【转载请注明出处】chenrudan.github.io
随着神经网络算法的发展,网络性能虽然越来越强大,但是也耗费了太多的计算资源和内存,为了得到更有效率的网络以及能部署在移动端,近几年神经网络的压缩算法成了一个研究热点,主要的网络压缩途径有五种,量化、剪枝、低秩分解、教师-学生网络、轻量化网络设计,量化就是将以往用32bit或者64bit表达的浮点数用1bit、2bit占用较少内存空间的形式进行存储。剪枝的目的是为了去掉一些不重要的神经元、连接、通道等,低秩分解主要是通过各种分解方法用精简的张量来表达复杂张量,教师-学生网络间接通过提升小网络性能来压缩学生网络的规模,一般可以与其他压缩方法同时使用,轻量化网络设计主要是类似MobileNet这种设计的非常精简但性能又好的网络。几种方法都各有特点,都是值得研究和讨论的,本文主要针对量化算法近几年的发展做一个梳理和归纳,我觉得量化算法有几个特点,理论简单,公式少,性能稳定且trick多。
下图1-4我整理了本文涉及到的文章在各个开源数据集上的性能表现,由于各个文章中对比指标不是完全一致,例如MNIST、Cifar10所用到的基础网络不一定一样,对性能感兴趣的可以去对照原文看看。
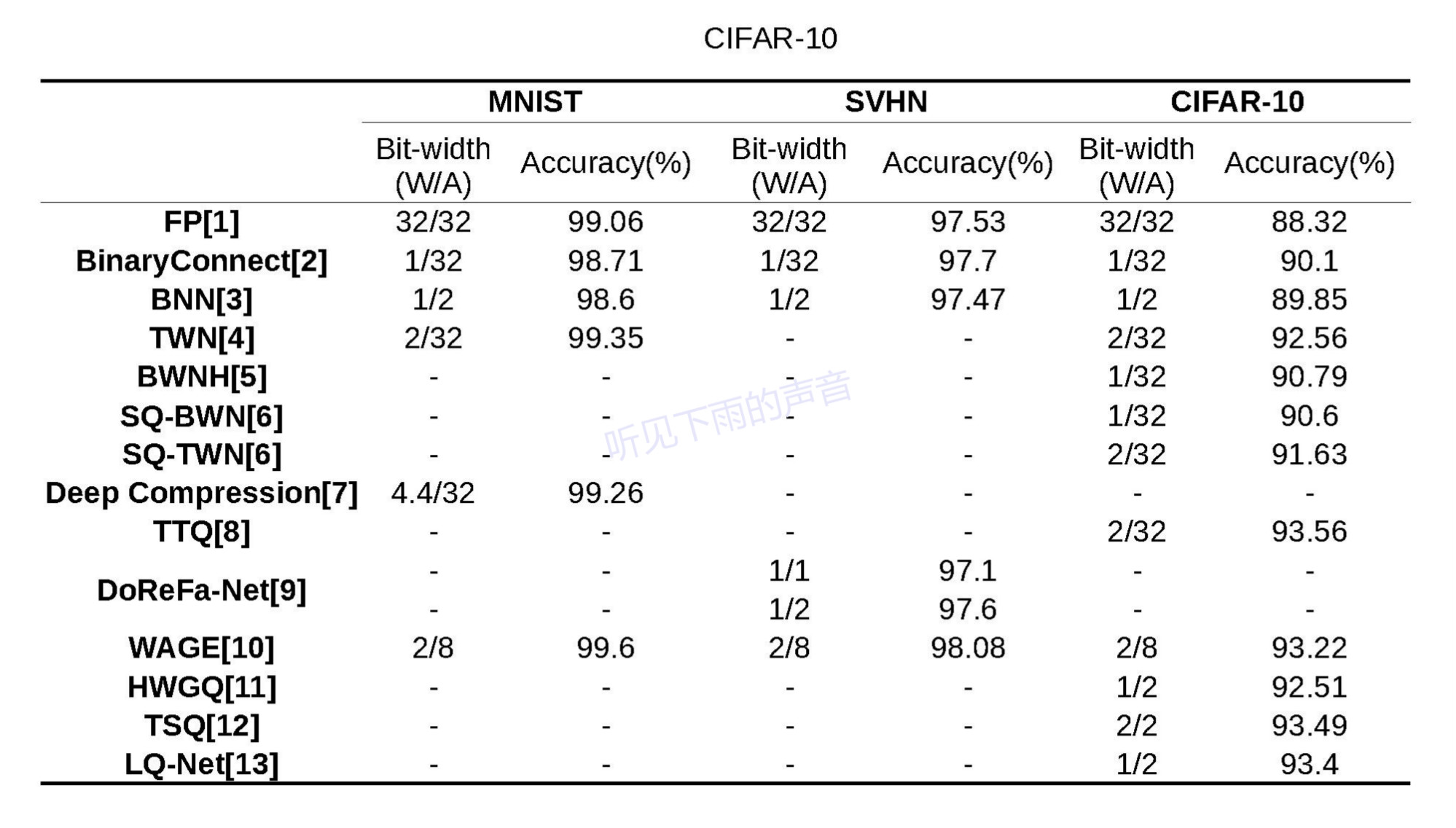 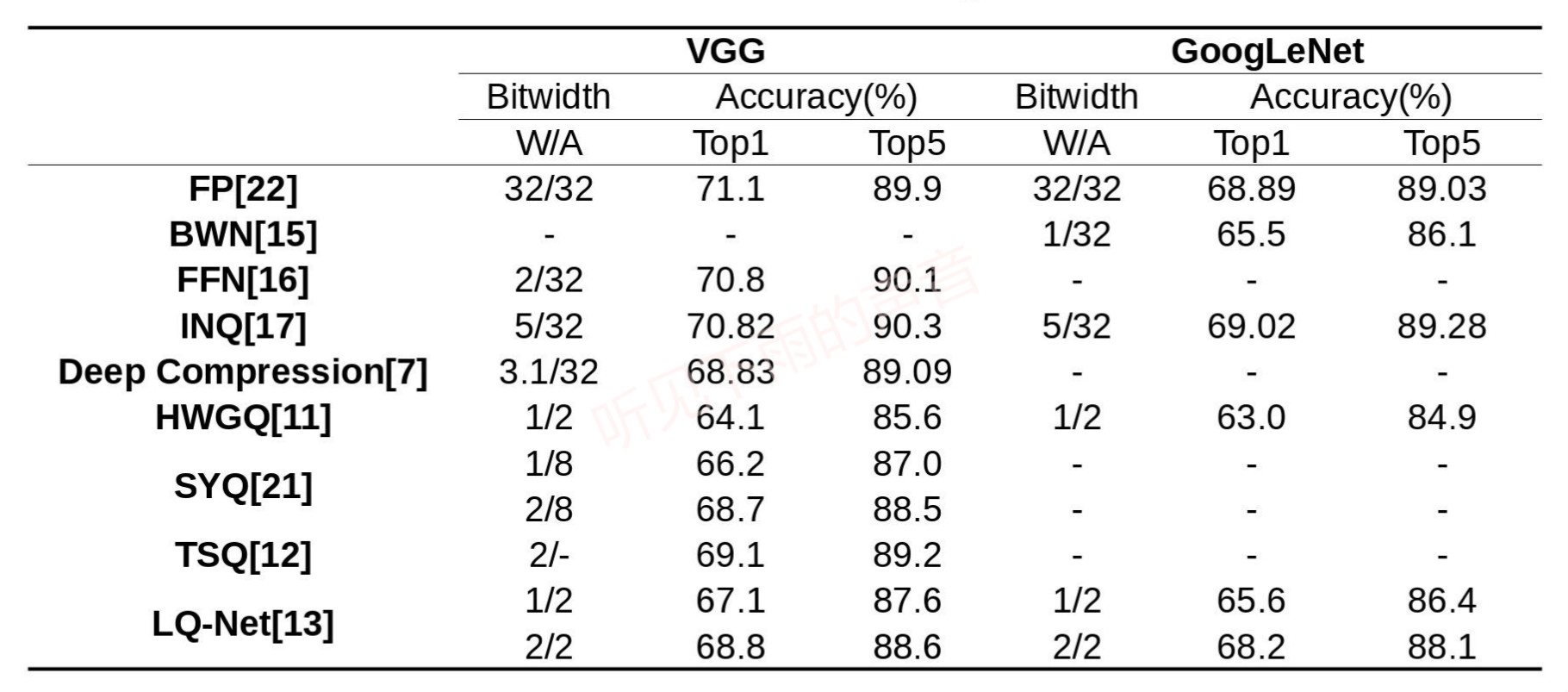 图1 Cifar10、VGG、GoogLeNet 图1 Cifar10、VGG、GoogLeNet | 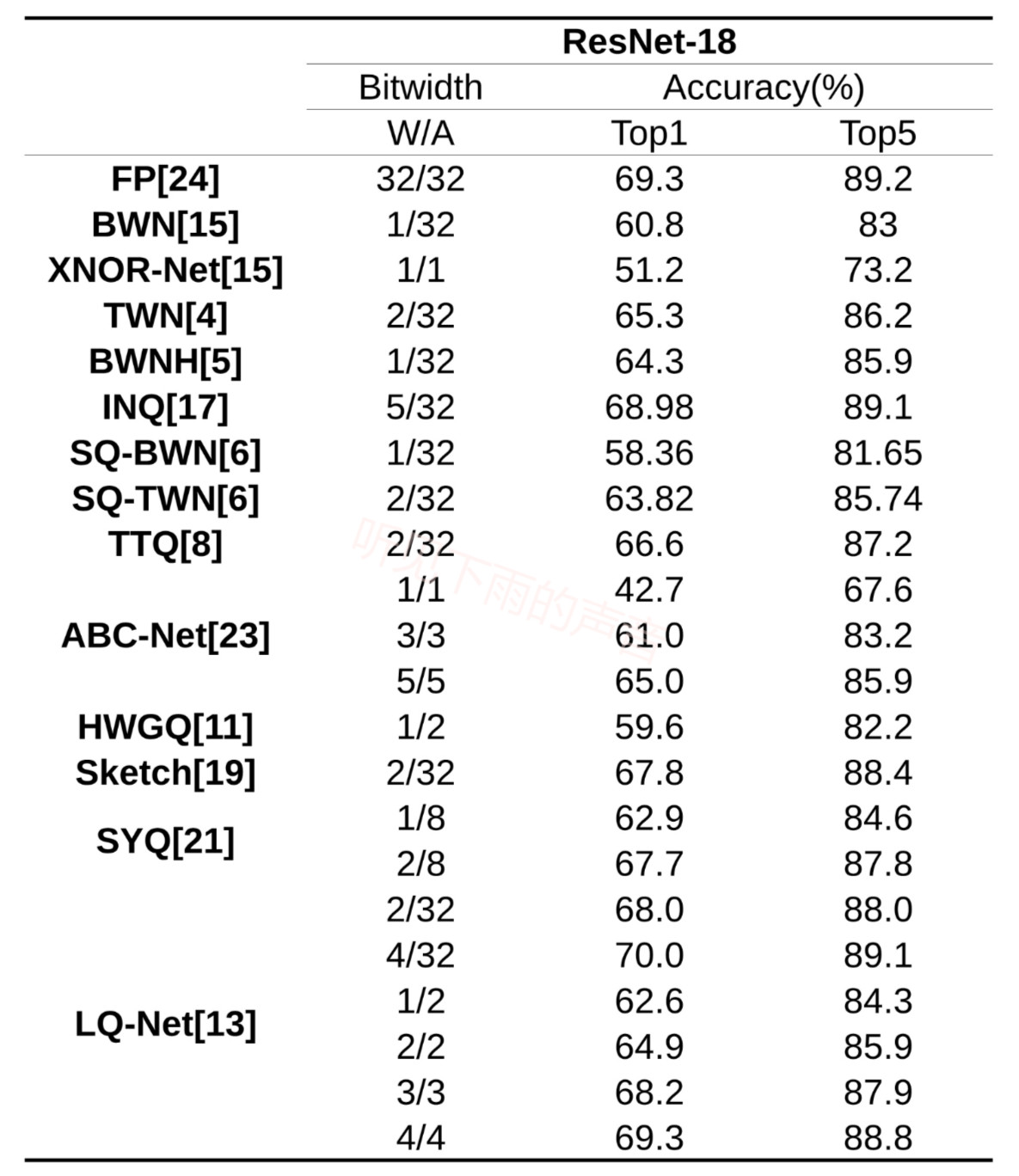 图2 AlexNet 图2 AlexNet |
 图3 ResNet18 图3 ResNet18 | 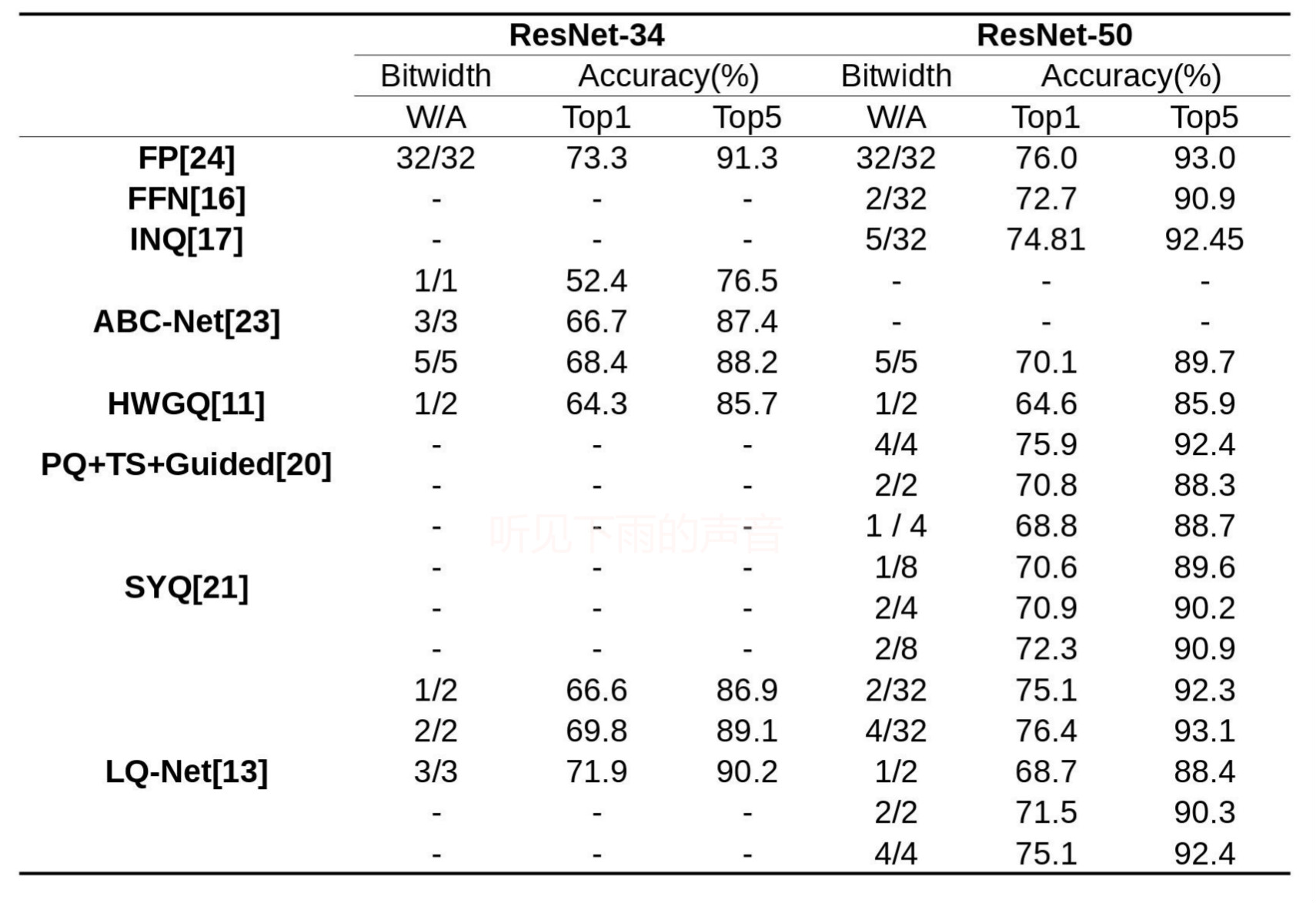 图4 ResNet34 & ResNet50 图4 ResNet34 & ResNet50 |
  图1 Cifar10、VGG、GoogLeNet 图1 Cifar10、VGG、GoogLeNet |  图2 AlexNet 图2 AlexNet |
 图3 ResNet18 图3 ResNet18 |  图4 ResNet34 & ResNet50 图4 ResNet34 & ResNet50 |
模型量化主要包括两个部分,一是针对权重Weight量化,一是针对激活值Activation量化,在一些文章中已经表明了将权重和激活值量化到8bit时就可以等价32bit的性能。在神经网络中的基本操作就是权重和激活值的卷积、乘加操作,$W*A$如果将其中一项量化到{-1,1},那么就将乘加操作简化为了加减操作,如果两项都量化到{-1,1},乘加操作就简化为了按位操作,对于硬件计算是非常友好的。
BinnaryConnect
BinnaryConnect[2]是我看到的第一篇归纳出完整量化流程的文章,它提出DNN的前向和反向训练中用1bit的二值权重替代浮点权重,能够让硬件计算将乘法操作简化成简单的累加操作,且能大量的减少存储空间,在MNIST、CIFAR-10、SVHN上接近SOA的性能。
我们知道正是由于神经网络参数量大,无法直接得到损失函数的最优参数,才采用了梯度下降的方式来逼近最优解,Sgd通过平均权重带来的梯度来得到一些小的带噪声的步长,尝试更新权重去搜索参数空间,因此这些梯度十分重要,要具有足够的分辨率,sgd至少需要68bits的精度,大脑突触的估计精度也是612bits。。如果采用量化权重,就会导致无法对权重直接求导,这种权重可以被看成是带噪声的权重。文章认为带噪声的权重往往能够带来正则化,使得泛化能力更好,类似dropout、dropconnect这种就是对激活值或者权重加入了噪声,它们表明只有权重的期望值需要是高精度的,添加噪声往往是有益处的,所以对权重进行量化理论角度是可行的,且在部分文章中发现对梯度随机取舍能够提供无偏离散化。
在本文中提出了BinaryConnect,在DNN的前向和反向训练中用二值权重替代浮点权重,此处的二值权重B取值为{-1,1},文章中提出了两种量化方法,判别式和随机式,其中$\sigma (w)=clip(\frac{x+1}{2},0,1)$,公式1通过符号函数直接取浮点权重的符号,公式2根据当前浮点权重求出一个概率,按照这个概率随机分配正负1。
$$
w_b= \begin{cases} +1, & \text {if $w \geq$ 0}; \ -1, & \text{otherwise} \end{cases} \tag{1}
$$
$$
w_b= \begin{cases} +1, & \text {with probability $p=\sigma (w)$}; \ -1, & \text{with probability 1-p} \end{cases} \tag{2}
$$
完整算法流程如下图5,C是损失函数,binarize(w)是按照上述公式二值化权重值,clip(w)是截断权重值,L是层数。前向传播时,只对权重做二值化,然后逐层求出二值权重得到的激活值,反向传播时,也是在二值权重上将对每层输入的导数传播回来,此时的导数是浮点的,更新参数时,同样求得的梯度也是浮点的。由于通常求得的梯度数值不是很大但是又非常重要,所以此处参数更新时还是用浮点梯度。由于权重量化时只取符号,浮点权重大于正负1,对结果没有影响,为了限制浮点权重不会增长过于夸张以及提高正则性,使用了clip函数将浮点权重限制在正负1之间。
 图5 BinnaryConnect算法流程
图5 BinnaryConnect算法流程 图5 BinnaryConnect算法流程
图5 BinnaryConnect算法流程量化网络如何inference,一是直接用二值权重。二是用浮点权重,权重二值化只用在训练阶段。三是从浮点权重和随机二值化可以采样出很多二值网络,将它们的预测输出平均一下作为输出。论文用第三种方法,训练过程中用随机二值权重,测试时用浮点权重可以提升性能,证明了论文前面认为的带噪声的权重具有一定的正则性。
这篇文章主要贡献在于将浮点权重量化到1bit,提出了完整的量化权重流程,且从带噪声的权重角度来解释量化权重。
BNN
BNN[3]与BinnaryConnect是同一个作者,也是这个算法的扩展,在前面只将权重量化到了1bit,本文则进一步将激活值也变成1bit,即减少了内存消耗,也将许多乘加操作简化成了按位操作XNOR-Count,二值化CNN能够减少60%的硬件时间复杂度,训练BNN在MNIST、CIFAR-10、SVHN上达到了SOA的性能。
权重和激活值都量化成了{-1,1},量化方式也是按照公式1和2,随机式在硬件实现上具有一定的难度,为了加快训练速度,文章中用的是判别式。由于符号函数的梯度都是0,离散神经元的梯度可以通过straight-through estimator[25]来解决,即浮点数的梯度等于量化数的梯度$g_r = g_q1_{|r|\leq 1}$,但是如果浮点权重数值过大,一般要舍弃掉这个梯度。
在训练过程中,需要保存二值权重和浮点权重,在前向后向计算中用二值权重,计算出来的梯度保存成浮点,且更新到浮点权重上。前向传播时,先对$W_k$做二值化,然后与当前的二值输入$a_{k-1}^b$,相乘得到$s_k$,再经过BatchNorm,得到输出即下一层的输入$a_k^b$。反向传播时,对二值激活值的的梯度等于对浮点激活值的梯度,计算对上一层输入的梯度时用的是二值权重,计算对二值权重的梯度时用的是上一层的二值激活值。在更新梯度时,梯度更新在浮点权重上,并将新一轮的$W_k^{t+1}$限制在-1~1之间。
文章中提出了第一个卷积层参数普遍较少,所以第一个卷积层输入量化到8bit,后面很多论文也采用同样的策略。与1bit权重相乘方式如公式3,$x^n$代表的是用8bit表示方法第n位的取值。
$$
s = \sum_{n=1}^{8}2^{n-1}(x^n\cdot w^b) \tag{3}
$$
BNN算法主要贡献在于同时对权重和激活值量化到1bit,不仅从实验角度证明量化算法的可行,还分析针对低bit如何进行更有效的计算,整理出了同时量化权重和激活值到1bit的算法流程,且针对内部的硬件计算,给出了具体实现,例如Shift-based Batch Normalization、XNOR-Count,最终训练能减少60%的时间,32倍的存储空间。
XNOR-Net
这篇文章[15]提出了两个网络Binary-Weight-Networks(BWN)和XNOR-Net,BWN只将权重量化为二值,XNOR权重和激活值都是二值,速度快了58x,内存节省32x。当AlexNet压缩成BWN时,性能与浮点网络一致。
在对浮点值进行量化时,加入了一个scaling factor,例如权重量化中$W=\alpha B$,$\alpha$是一个浮点实数,所以在BWN中权重取值就是$-\alpha, +\alpha$,所以量化变成了一个优化问题,这个优化问题是公式4,找到最优的$\alpha$使得量化权重与浮点权重之间差距最小。
$$
J(B,\alpha )=||W-\alpha B||^2 \
\alpha^{*},B^{*}=\underset{\alpha,B}{argmin}J(B,\alpha ) \tag{4}
$$
将公式4对$\alpha$求导再设为0,得到alpha的解析解$ \alpha^{*} =\frac{W^TB^{*}}{n} $,其中包含了二值权重B,如果假设B通过符号函数来求解,那么可以推导出$ \alpha^{*} =\frac{1}{n} ||W||_{l_1}$。
XNOR-Net中对激活值也量化$X = \beta H$,其中H也是{-1,1},$\beta$是它的尺度系数,卷积包括重复shift操作和点乘,shift指的是filter在输入图上进行移动,当输入输出都变为二值时,将权重和激活值的尺度系数提取出来之后,卷积可以变成xnor-bitcounting操作。
Cnn训练分为三个部分,前向传播、后向传播、参数更新,在前向后向的计算中使用量化权重,更新时如果直接更新量化权重,那么梯度可能不够大到改变量化权重的取值,所以还是让浮点权重进行更新。
XNOR-Net文章主要贡献在于提出了一个更好的拟合浮点数的方法,即给二值数增加一个尺度因子,而不是简单的取符号,在alexnet上将权重量化到1bit时能够达到跟浮点权重一样的性能。
TWN
前几篇文章都是将浮点数直接量化到了1bit,TWN[4]则提出将权重量化成2bit,虽然2bit能表达四个数,但是只取了三个数{-1,0,1},在mnist和cifar10数据集上三值权重性能比二值权重好很多,通过2bit表达,可以达到16x到32x的模型压缩比例。
一般卷积kernel的尺寸是3x3,针对二值权重,表达能力是2^(33)=512种配置,而三值权重3^(33)=19683种配置,所以说三值权重比二值权重的表达能力要高很多。三值权重取值上多了一个0,实际计算中,由于0值处不需要进行相乘累加,对硬件也是十分友好。
量化公式如公式5,也使用到了尺度因子来拟合浮点权重,最小化量化权重TWN和浮点权重FPWN之间的L2距离。
$$
\alpha^{*},W^{t*}=\underset{\alpha, W^t}{argmin}J(\alpha, W^t)=||W-\alpha W^t||^2 \text { s.t. } \alpha\geq 0, W_i^t\in {-1,0,1} \tag{5}
$$
优化问题就变成了如何求出$\alpha$和$W^t$,同样对$\alpha$求梯度且令梯度为0,可以得到$\alpha$的解析解,求出来的$W^t$和$\alpha$是相互关联的,所以无法直接得出,文章就提出了一种量化方法,首先需要一个阈值$\Delta$,这个阈值用来区分浮点权值映射到正负1、0上,如公式6。然后求出的$\alpha_{\Delta}^{*}=\frac{1}{|I_{\Delta}|}\sum_{i\in\Delta}|W_i|$。
$$
W_i^t=
+1, :::if:: W_i > \Delta \\
0, :::if:: |W_i| \leq \Delta \\
-1, :::if:: W_i < -\Delta \tag{6}
$$
求阈值则无法直接去求解,因此假设权重服从几个分布来分析这个阈值的求解途径,例如假设权重服从均匀分布[-a,a],阈值$\Delta=1/3*a$,例如服从高斯分布,阈值$\Delta=0.6\sigma$,所以作者归纳出了一个经验公式用于求解$\Delta^{*}=\frac{0.7}{n}\sum_{i=1}^n|W_i|$,然后求出对应$\alpha$。训练网络的方式与之前的文章一致。
TWN的主要贡献通过2bit来近似浮点权重,相比于二值权重性能有较明显的提升,但由于取值也限于正负1和0,对硬件计算没有额外的负担。
BWNH
[5]认为量化的过程可以看成一个hash映射,目标就变成了交替优化方法来学习哈希码。
在之前文章中的量化优化问题都是找到最优的量化数值来拟合浮点数值,本文中考虑的是最小化内积的量化误差。本文中是将权重量化到1bit,内积指的是权重和激活值之间相乘,也称为输入X和权重W的相似性矩阵$S=X^TW$,将浮点权重映射到量化权重的哈希函数为$B=g(W)$,哈希函数$X=h(X)$,h是恒等映射函数。
$$
minL(B)=||X^TW-X^TB||_F^2:::s.t. B\in\{+1,-1\}^{S\times N}\tag{7}
$$
$g(W)=BA$,A是对角矩阵,每个元素是一个scaling factor,所以目标函数也可以写成$minL(A,B)=\sum_i^N||S_i-\alpha_i\cdot X^TB_i||_F^2$,计算每个$\alpha$、输入、二值权重之间的乘积来拟合浮点权重与输入乘积,要求的是哈希映射g,将浮点权重映射到正负1、0这样的hash code上。
此处对A和B求梯度设为0,可以推导出带有输入数据关于$\alpha$和B的求解公式8,在更新A时将B固定不动,更新B时固定A不动,且更新每一个B时还要固定剩下的B,即通过这种交替优化的方式来进行更新。且由于二值权重的量化error是网络层与层从头到尾一直在累加的,因而考虑分层量化,例如先对前l个层做二值化,让整个网络逐渐的适应二值权重,再去量化第二个部分。
$$
\alpha_i = \frac{S_i^TX^TB_i}{||X^TB_i||_F^2} \
b=sign(q_j-B_i^{‘T}Z^{‘}v) \tag{8}
$$
在具体算法流程中,逐层的对每一层的权值做二值化,每一层量化时初始化时B取浮点权重的符号,而A取权重平均绝对值,接着就按照公式8进行交替的优化A和B。最后再对整个网络进行finetuing。
BWNH只对权重进行了量化,算法主要贡献在于从哈希角度来解决量化问题,并且提出了逐层的交替更新,相对于之前的二值权重量化方法性能有着较为明显的提升。
FFN
FFN[16]中只将浮点权重量化到2bit,通过定点化分解方式来求解量化后权重,由于三值权重只有正负1和0,即可以消除最耗费资源的multiply-accumulate operations(MAC)操作,FFN可以得到浮点网络性能相当的网络,且乘法运算仅为浮点网络的千分之一。
通过semidiscrete decomposition(SDD)半离散分解将浮点权重W分解成定点化方式$W=XDY^T$,中D是一个非负对角矩阵,X和Y每个元素取值为{-1,0,1},所以一个正常的卷积n*c*h*w会被分解成三个步骤,卷积有n个输出channel,拆成三个后,第一个可看成有k个输出channel的卷积,即k*c*h*w,第二个步骤相当于每个特征图都乘以一个尺度因子,最后一个也可以看成卷积层大小是n*1*1*k。
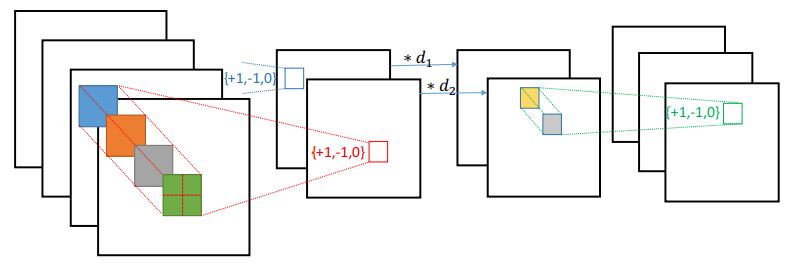 图6 FFN分解
图6 FFN分解 图6 FFN分解
图6 FFN分解为了更好的恢复浮点权重,算法中保留了X和Y对应的浮点数值$\hat{X}$和$\hat{Y}$,且浮点数值被限制在-1.5~1.5,根据取值落在哪个区间量化到哪个数值,而在梯度更新时,更新的对象是$\hat{X}$和$\hat{Y}$。
FFN只针对权重做了量化,提出了将浮点权重矩阵用矩阵分解的方式分解成三个简单矩阵,其中两个矩阵元素取值为正负1和0,从而间接完成量化的功能。
INQ
INQ[17]提出增量网络量化方法,通过权重分组、按组量化、重新训练三个操作将浮点网络量化到低bit网络,在resnet18上量化权重后,4bit、3bit、2bit能够达到甚至超过浮点权重。
文章从网络剪枝算法中得到灵感,逐步的从已经训练好的网络中移除掉不那么重要的权重,最终性能也不会有明显下降,所以说权重是存在不同的重要性的,但是之前的方法没有考虑到这点,而是同时将高精度浮点数转化为低精度数值,因此改变网络权重的重要性对于减少量化网络的损失很重要。
本文中低bit权重需要一个符号位,至少从2bit开始,b是比特数,取值范围是$P_l={\pm 2^{n_1},…,\pm 2^{n_2},0}$,由两个整数n1n2定义$n_2 = n_1+1-\frac{2^{b-1}}{2}$,通过经验公式可以计算出n1n2。量化公式9中的$\alpha$和$\beta$就是$P_l$中相邻的两项。
$$
\hat{W_l}(i,j)=\beta sgn(W_l(i,j)) :::: \text{if}(\alpha+\beta)/2\leq abs(W_l(i,j))< 3\beta/2 \
0, otherwise \tag{9}
$$
网络训练过程中,将权重分割到两个不相交的组中,第一个组$A_l^{(1)}$中的权重基于公式4进行组内量化,另一个组$A_l^{(2)}中权重保持浮点精度,自适应的弥补量化模型造成的loss,且在反向re-training更新权重时,通过一个mask来判断属于哪个组,属于第一个组的量化权重就不更新,只更新第二个组的浮点权重。然后针对第二个组的浮点权重做重复的三步操作,直到所有权重被量化完成。
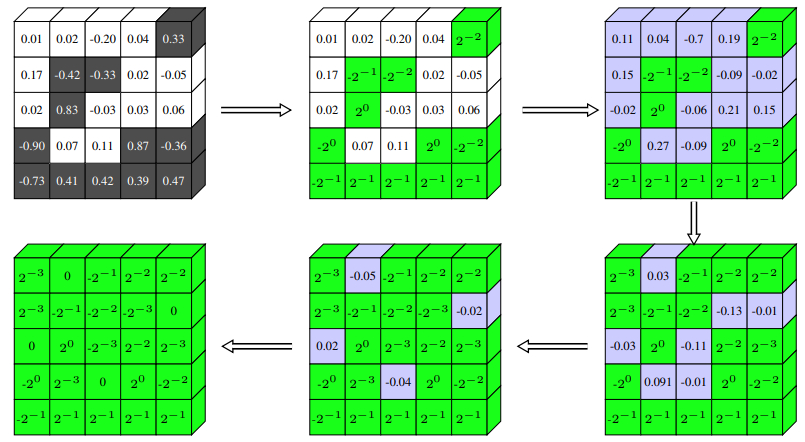 图7 INQ算法
图7 INQ算法 图7 INQ算法
图7 INQ算法INQ算法对权重进行了量化,通过逐步增量式的将权重量化,通过保留一部分浮点权重来恢复模型的性能,精度损失得到了一定的遏止。
SQ-B(T)WN
SQ-B(T)WN[6]也是一种增量式量化算法,它从不同权重会导致不同量化误差角度,在近似实数权重时,可能只是针对部分filter量化error大,部分filter量化error小,文章提出了随机选择部分filter量化STOCHASTIC QUANTIZATION,逐渐增加量化比例最终完成全部权重量化。
一层的权重按照输出channel作为一组数据$W={W_1,…,W_m}$,其中m等于输出channel数量,第i个filter权重是$W_i$。也是将这一层的权重划分成两个不相交的集合$G_q$和$G_r$,将$G_q$中权重量化到低bit,而$G_r$权重还是浮点,$G_q$有$N_q=r*m$个filter,而$G_q$有$N_q=(1-r)*m$个。其中r就是随机量化SQ比例,r在逐渐增加,最终增加到1。
针对每一个filter$W_i$都有自己的一个量化概率$p_i$,表明第i个filter被量化的概率,量化概率的取值由量化误差决定。当量化误差小时,量化当前的这个channel就会造成较少不同的信息损失,那么就能给这个channel赋予较大的量化概率。首先定义浮点权重和量化权重的L1距离$e_i=\frac{||W_i-Q_i||_1}{||W_i||_1}$,将它作为量化误差,并定义一个中间变量$f_i=\frac{1}{e_i+\epsilon }$,从而量化概率可以有不同的求解方法,例如$p_i=1/m$或者$p_i=\frac{1}{1+exp(-f_i)}$。
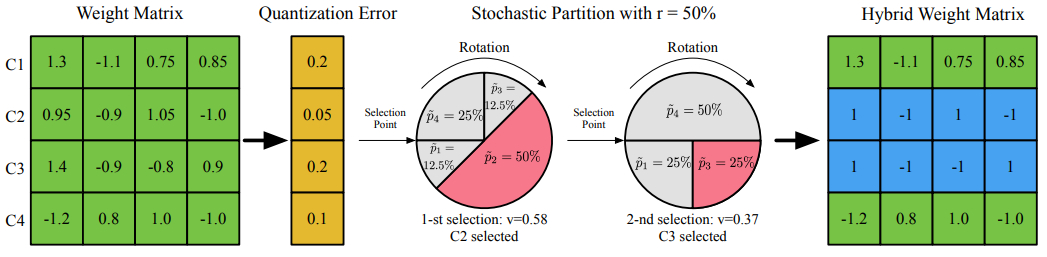 图8 随机channel量化
图8 随机channel量化 图8 随机channel量化
图8 随机channel量化在图8中,先计算出4个channel的量化error,假设当前r=50%,根据每个channel计算出来的量化概率挑选2个channel量化。
SQ-B(T)WN算法通过逐步量化权重,比直接全部量化产生的更加合适梯度方向,但是从算法结果上来说,看起来并不是特别好。
Deep Compression
Deep Compression算法[7]结合了剪枝、量化、哈夫曼编码三种操作,在性能没有降低的情况下压缩了35x~49x,目标是减少存储空间减少inference的耗时,从而能部署在移动设备上。
第一步是剪枝,在训练过程中来学习各个连接的性能表现,然后裁剪掉权重较小不够重要的连接,通过设定一个阈值,小于这个阈值移除掉,再重新训练留下的稀疏连接。剪枝后的稀疏结构用compressed sparse row和compressed sparse row方式存储,需要保存2a+n+1数据,a是非零值元素个数,n是行数或者列数。这一步中可以在Alexnet和VGG-16上压缩9x~13x。
第二步是量化,通过让多个连接共享相同权重来达到量化目的,在有限的bit数中只能表达有限的数值,所以当某些神经元取一样的数值时,就说它们在共享这个权重。假设权重大小是4*4,权重被量化到4个bin,在相同bin中的权重取值相同,因此只需要保存bin的索引,更新的时候相同bin中的梯度加起来再更新。假如有k个bin,那么需要log2k位来对索引进行编码,假如网络有n个连接,每个连接由b个位表达,从而可以得到压缩比例$r=\frac{nb}{nlog2(k)+kb}$。通过k-means聚类来确定这些用于共享的权重,将n个权值分配到k个类中,最小化权重和类中心绝对值之差(WCSS)得到类中心$C={c_1,…,c_k}$。尝试了三种初始化共享权重中心C的方法,随机、基于密度、线性初始化,随机方法就从权重中随机选择k个值,基于密度会选择一些在尖峰周围的点,线性初始化在权重数值线性进行间隔选择,发现线性初始化效果最好。反向传播也跟其他量化方式是一致的。
huffman编码是一种无损数据压缩方法,压缩非均匀分布的值可节省20%30%的网络存储。最终经过这三个操作,网络在性能没有降低的情况下被压缩了35x49x。
这篇文章操作较多比较复杂,但是性能是稳定可靠的,每个压缩操作都没有导致性能下降。
TTQ
TTQ[8]量化浮点权重到三值权重,在开源数据集上相比浮点性能下降很少。
在之前的量化算法中,是通过一个尺度因子和三值权重相乘来拟合浮点权重,像在TWN中给出了经验公式来计算尺度因子$\alpha$,本文提出了通过梯度下降对$\alpha$进行更新。
首先将浮点权重除以最大值后正则化到正负1之间,所有的层有一个相同的参数t,用来计算阈值$\Delta_l = t \times max(|\tilde{w}|)$进行量化。
$$
w_l^t=W_l^p:\tilde{w}_l>\Delta_l \
0:|\tilde{w}_l|<\Delta_l \
-W_l^n:\tilde{w}_l<-\Delta_l \tag{10}
$$
这里针对正负数有不同的量化levels,即有两个尺度因子$W_l^p$和$W_l^n$。因此对它们计算梯度可以得到梯度下降更新公式,$\frac{\partial L}{\partial W_l^p} = \sum _{i\in I_l^p}\frac{\partial L}{\partial w_l^t(i)},\frac{\partial L}{\partial W_l^n} = \sum _{i\in I_l^n}\frac{\partial L}{\partial w_l^t(i)}$。在观察尺度因子的变化情况时,针对第一个量化全局层,正负尺度因子的绝对值会变得越来越小,稀疏性降低了,针对最后一个卷积层和全连接层正负尺度因子的绝对值会变得越来越大,稀疏性提升了。
对尺度因子进行训练的好处在于,正负尺度因子的不对称使得模型能力更强,且针对所有层有一个常数稀疏r,调整超参数r可以调整量化阈值,能够获得不同稀疏度的三值网络。
TTQ中将正负量化levels分开考虑,且作为可训练的参数进行更新,而不是用经验公式进行计算,性能比TWN也要好一些。
DoReFa-Net
在DoReFa-Net[9]中权重、激活值和参数梯度都设置成了低bit,优点是不只在inference时能够加速,且训练时由于梯度也被量化了,训练时也能加速。所以能够很好的在硬件平台上直接进行训练。
当权重和激活值都量化后,就能够用bitcount操作来计算,即x和y相与的结果后可以直接数出位置为1的个数,而之前的文章中还没有量化过梯度到8bit以下。在BNN网络中,浮点梯度在-1到1范围内时等于量化梯度,超出范围就等于0,在xnor-net中,浮点梯度直接等于量化梯度,由于加上了一个尺度因子,所以权重能够表示的范围就更广了,在DoReFa-Net中权重量化方式为$r_o = f_w^k(r_i)=2quantize_k(\frac{tanh(r_i)}{2max(|tanh(r_i)|)}+\frac{1}{2})-1$,其中k是指定的bit数,$f_w^k(r_i)$取值被限制在了-1~1之间。
激活值的量化先是由一个激活函数将范围限制在0~1之内,再量化到k bit,$ f_a^k(r)=quantize_k(r)$。
在针对梯度进行量化时,随机量化是一个比较有效的手段,且梯度是不像激活值可以被限制在某个范围内,有的位置上梯度取值可能会比较大,激活值由于可以经过一个激活函数,所以能够限制数值大小。梯度量化公式为$ f_\gamma ^k(dr)= 2max_0(|d_r|)[ quantize_k[\frac{d_r}{2max_0(|d_r|)}+\frac{1}{2}+N(k)]-\frac{1}{2}]$,本文的随机就体现在加入了一个额外的噪声函数$N(k)$,效果非常明显。
所以DoReFa-Net并不是指定量化到多少bit,而是可以量化到任意的bit,由于整个网络的输入数据层channel较少,对于整体网络复杂度影响较小,因此第一个卷积层的权重不进行量化,第一个卷积层的输出激活值会被量化,如果输出类别较少时,最后一个卷积层的权重也不进行量化,最后一层的反向梯度需要量化。
这篇文章主要就是提出对梯度也进行量化,并且支持量化到任意bit。
ABC-Net
二值权重和激活值能够很大程度的减少内存空间,且能采用按位计算,对硬件很友好,但是现有的方法会导致性能下降,本文主要提出了ABC-net(Accurate-Binary Convolutional)线性组合多个二值权重基来拟合浮点权重,利用多个二值激活值基组合来减少信息损失。
将浮点权重用M组二值权重和尺度因子进行线性组合,$W\approx \alpha_1 B_1+\alpha_2 B_2+…+\alpha_M B_M$,将B表示成浮点权重与均值和方差的组合形式$B_i = F_{u_i}(W):=sign(W-mean(W)+u_istd(W))$,其中有一个尺度变量$u_i$,既可以由经验公式$u_i=-1+(i-1)\frac{2}{M-1}$直接算出,也可以通过网络训练的方式得到。这样去估计B的原因是,浮点权重倾向于是一个对称、非稀疏分布,比较类似高斯分布,所以用均值和方差来估计。确定B之后,通过线性回归来求解alpha。在增加了尺度因子后,求解反向梯度时,会增加一个$\alpha$系数,$\frac{\partial c}{\partial W} = \sum_{m=1}^{M}\alpha_m\frac{\partial c}{\partial B_m}$。在实现中,将浮点权重按照channel区分开,用同样的方式来估计尺度因子和二值权重,理论上能够更加细致的拟合浮点权重。
当权重是二值的,卷积操作就没有了乘法,只剩下加减,如果想要更高效的利用按位操作,最好是将激活值也变为二值。因此类似对权重的处理,文章首先将激活值通过一个clip函数$h_v(x)=clip(x+v,0,1)$,将范围限制在0~1之间,量化激活值取值是{-1,1},通过一个指示函数$A=H_v(R):=2\mathbb{I}_{h_v(R)\geq 0.5}-1$进行量化,量化激活值与量化权重的不同点在于,inference的阶段权重是不变的,激活值则变化了,但是通过利用神经网络激活值的统计特性能够避免这个问题,为了保证激活值的分布相对稳定,使用了batchnorm,它能够让输出保持0均值1方差的分布。用N组二值激活值和尺度因子组合成浮点激活值$R\approx \beta_1A_1+\beta_2A_2+…+\beta_NA_N$,激活值量化中多了一个可以训练的阈值$v$。卷积操作就转化M*N个按位操作,$Conv(W,R)\approx \sum_{m=1}^{M}\sum_{n=1}^{N}\alpha_m\beta_nConv(B_m,A_n)$。
ABC-Net也是一个不限制bit数的量化算法,性能也接近浮点网络。
HWGQ
HWGQ[11]主要针对激活值量化,利用了激活值的统计特性和batchnorm操作,在前向计算时能有效的近似浮点值的性能。
针对激活值的量化需要处理不可微的操作,主要切入点在于ReLU函数,神经网络每个单元都计算了一个激活函数,即权重与输入相乘后经过一个非线性变换,这个操作的多少决定了整个网络的复杂度。
本文中估计1bit量化权重,也是基于二值权重和尺度因子相乘去拟合浮点权重,输入I与量化权重卷积来近似I和浮点权重卷积结果,是二值权重取浮点权重的符号$B^*=sign(W)$,尺度因子是浮点权重平均绝对值$\alpha^*=\frac{1}{cwh}||W||_1$,1bit权重能够减少存储空间,但是无法完全计算复杂度的问题,如果将I也变成二值的,则能够最大程度上解决计算复杂度的问题。
在对激活值进行量化时,如果直接按照符号函数来定义量化levels,那么对量化激活值进行求导时,导数处处为0,所以有人提出,对符号函数求导如果输入绝对值小于1则梯度为1,其他位置取0。结合relu函数,本文对激活值量化的目标是拟合relu函数的输出。quantizer是一个分段常数函数,量化levels就是量化到的值,量化step就是两个量化level之间的差,针对每个浮点数值,它只需要保存一个索引值i,对应到第i个量化level,非均匀量化情况下表达浮点权重需要多余$log_2m$的bit数,如果是均匀量化则$log_2m$个bit就够了。激活值的统计结构倾向于对称非稀疏分布类似高斯分布,再结合relu,就是变成了一个半波高斯量化子half-wave Gaussian quantizer。这里的量化就是变成了求针对高斯分布的量化levels和step,但是在不同层的神经元所得到的类高斯分布,它们的均值方差不一定是相同的,为了得到相同的数据分布,通过batchnorm来得到0均值1方差的分布,然后就能在神经元之间得到均匀的量化参数。以上是在解释构造这样的HWGQ,它是阶梯常数函数,梯度处处为0,目标就变成了选哪个函数作为HWGQ在量化后才能最好的拟合relu函数的效果。
首先考虑最基本的relu函数,它对输入的梯度等于输出梯度,与正向的HWGQ所需要的梯度是不匹配的,特别是当输入数值大于最大的量化level时,产生的误差导致的反向梯度就会特别大。基于这个情况,考虑用clipped后的relu,保证最大值不超过最大的量化level,但是由于clipped的操作,丢失掉了$q_m$之后的输入信息会直接导致性能的下降,因此提出一种折中的函数公式11即长尾relu,它既能保证超过$q_m$的梯度不会过大,也不会完全丢失掉大于$q_m$的信息。
$$
\tilde{Q_l}(x)=q_m+log(x-\tau ),x>q_m \
x,x\in (0,q_m] \
0,x\leq 0 \tag{11}
$$
HWGQ主要从理论上分析如何去选择一个激活函数,从而保证激活值量化后低bit网络性能接近浮点网络。
Network Sketching
本文提出了Network Sketching[19]用来寻找量化二值权重的网络,整个过程可以看成是由粗到细的模型近似。
按照输出channel来划分不同的filter,假设有m组基来拟合一个channel的权重,$W=\sum_{m=0}^{m-1}\alpha_jB_j$,其中$B\in \{+1,-1\}^{c\times w\times h\times m}$,而$\alpha \in \mathbb{R}^m$。主要想法是基于不断拟合量化权重和浮点权重之间的残差,即计算浮点权重减去已经累加得到的量化权重$\sum_{k=0}^{j-1}\alpha_kB_k$之间的残差成为新的需要拟合的浮点权重,去获得下一步的B和$\alpha$,即公式12。
$$
\hat{W_j}=W-\sum_{k=0}^{j-1}\alpha_kB_k \tag{12}
$$
具体在求B和$\alpha$,B是取浮点权重的符号,$\alpha$由二值权重和浮点权重内积求出来$\alpha_j=\frac{ < B_j,\hat{W_j} > }{t}$,其中$t=c\times w \times h$。在第一个Direct Approximation算法中就是重复m次,求出m组B和$\alpha$。重构error以1/t的指数进行衰减,如果t取值小,重构error就会越小,t很大时,重构error的减少幅度就会很慢,就算增加m的数量,最终的近似效果可能也不够好。所以B和$\alpha$不一定是最优的,为了进一步优化得到更好的近似效果,在第二个Approximation with Refinement算法中给出更新公式,$a_j=(B_j^TB_j)^{-1}B_j^T\cdot vec(W)$,且文中进一步证明了更新公式能够近似浮点权重,减少量化error。
本文的sketch就体现在第j个量化权重是在估计当前浮点权重的残差,量化error越来越精细,就像在逐步的从粗到细描绘出具体的轮廓。
PQ+TS+Guided
本文[20]为了提升量化网络训练性能,提出了三个方法,一是两步优化策略,先量化权重再量化激活值,其次在训练过程中逐步减少量化位宽,第三联合训练浮点网络和低精度网络。
量化采用的是Q函数均匀量化,$z_q=Q(z_r)=\frac{1}{2^k-1}round((2^k-1)z_r)$,在量化权重时,先对w做归一化,其中tanh可以减少大值的影响,再用Q函数去量化,求解形式与DoReFa-Net是一样的。针对激活值,先将激活值通过clip函数限制在0~1的范围内,然后用Q量化。反向传播更新梯度也是基于STE算法。
为了增加量化的准确性,本文首先提出了两步优化two-stage optimization(TS),先量化权重再量化激活值,如果从K-bit的网络量化得到k-bit的网络,首先训练在K-bit激活值下的k-bit权重,在k-bit权重训练好后训练k-bit的激活值。而由于训练过程中近似的梯度不一定是准确的,所以会导致陷入局部最优值的情况,所以本文提出了分阶段量化progressive quantization(PQ)的想法,逐步减少量化位宽的方法,例如32bit->16bit->4bit->2bit,量化n次就得完整训练n次。第三个提升方法是基于教师-学生网络(Guided),联合训练浮点网络和低精度网络,互相适应,因为直接用固定的预训练好的浮点模型来指导量化网络不一定最好,且在特征图层面上进行迁移,为了保持浮点网络和低精度网络一致,在相互适应时,将浮点网络也做同样的量化,然后再相互迁移。
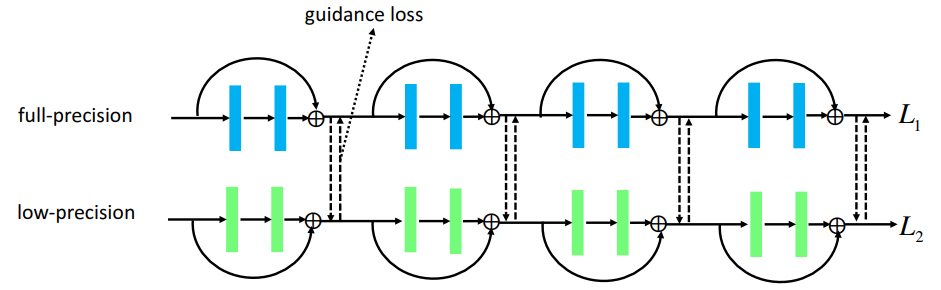 图9 Guided训练
图9 Guided训练 图9 Guided训练
图9 Guided训练这个方法主要是提出一些有效的trick来辅助训练量化网络,且表现非常不错。
SYQ
SYQ[21]提出了对称量化能够提升网络准确率。
在SYQ中,Codebook C是量化levels的一些可能取值,例如{-1,1},或者{-1,0,1},二值化或者三值化权重时通常的方法是采用分段常数函数,并存在$\eta$这样的量化阈值超参数,二值化时取为0,三值时由经验公式$\eta=0.05\times max(|W_l|)$得出。后来的估计方式中引入了scaling factor,提高了近似浮点数的能力,此时的codebook就变成了${-\alpha,\alpha}$,前面提到过的TTQ就是提出可以对$\alpha$进行训练,且设置正负两个尺度因子${-\alpha_l^n, \alpha_l^p}$,但是如果采用正负不同的尺度因子,那么在计算权重和激活值乘积时需要先去判断当前二值权重或者三值权重的符号,增加了额外的判断分支,所以本文认为对称的codebook计算效率会更高,codebook最好是在0周围对称,那存储空间可减半。
很多细粒度量化方法能够提升近似权重分布的能力,本文实现了按像素进行缩放,假设一层权重是$K\times K \times N \times I$,pixel-wise就是在I*N维度上将权重进行分组,此时$\alpha$个数为$K^2$,此时就是将权重分为了$K^2$组,row-wise将一个kernel中行或者列组成一组,最粗粒度的是layer-wise,一层只有一个$\alpha$。
在SYQ算法流程中,每一层首先通过$Q_l=sign(W_l) \bigodot M_l$量化权重成二值或者三值,其中$M_l$是通过$\eta$计算得到,然后通过$G(x)=\frac{1}{2^f}floor((2^f)x+\frac{1}{2})$线性量化激活值,前向计算完成之后,通过$\frac{\partial E}{\partial W_{l_{i,j}}} = \alpha_{l}^i\frac{\partial E}{\partial Q_{l_{i,j}}} $来更新权重,通过$\frac{\partial E}{\partial x} = \frac{\partial E}{\partial G} $更新激活值,通过$\frac{\partial E}{\partial \alpha_{l}^i} = \sum_{j\in S_l^i} \frac{\partial E}{\partial W_{l_{i,j}}}$更新scaling factor。
SYQ相对于TTQ没有特别明显的改进,增加了$\alpha$的数量使得最终性能想比于TTQ有提升。
TSQ
之前方法中都是同时量化权重和激活值,TSQ[12]提出了先量化激活值再量化权重,针对激活值,提出了稀疏量化方法,文章认为网络压缩和加速中稀疏能起到很大作用,之前的文章中都很少研究这个方向,且稀疏性在特殊硬件上会更有效,而权重量化可以看成低bit非线性最小二乘回归问题,通过迭代方式求解。
得到低比特权重是transformations,得到低比特激活值是encodings。在encodings问题中,Relu函数本身就产生了50%的稀疏性,在attention机制的基本假设中,数值较大的激活值比数值较少的激活值更重要。所以将数值较小的正值变成0,这样量化算法能够更能关注到较大的数值,量化的会更精细。n-bit均匀量化子quantizer将浮点激活值映射到$2^n$个离散值,主要就是在于决定量化间隔$\Delta$和量化范围$t_i$。之前的HWGQ方法中是通过batchnorm层,输出分布就非常趋近于0均值1方差的高斯分布,因此每个层的$\Delta$和$t_i$是相同的。本文提出稀疏量化,不是将经过relu后的所有正值都进行量化,而是将不重要的数值先设置为0再量化,这个想法之前在网络剪枝中也有类似研究,也就是大值比小值更重要。所以给出了一个稀疏阈值$\epsilon$,得到新的求解激活值量化函数的公式13。
$$
Q_{\epsilon}^*(x)=\underset{Q_{\epsilon}}{argmax}E_{x\sim N(0,1),x>\epsilon }[(Q_{\epsilon}(x)-x)^2] \tag{13}
$$
对权重进行量化,假设上一层的输出是X,这一层的输出是Y,将权重量化的问题变成一个非线性最小平方回归问题,将浮点尺度因子$\alpha$看成一个对角矩阵,与输入X相乘之后再经过激活值量化最终去拟合浮点输出$\underset{\alpha,\hat{w}}{minimize} || y - Q_{\epsilon }(\alpha X^T\hat{w}) ||$。然后引入了一个辅助变量z,将两个量化过程区分开$\underset{\alpha,\hat{w},z}{minimize} || y - Q_{\epsilon }(z) | | +\lambda || z - \alpha X^T\hat{w} ||$,权重量化去拟合辅助变量z,激活值量化去拟合浮点输出。
在求解$\alpha$和w时,将优化问题展开之后,对$\alpha$进行求导且设置导数为0,可以直接得出$\alpha$的求解公式,然后将$\alpha$带入展开公式同样求出w的求解公式。由于w的维数较高,即m个像素点每个都需要进行计算,而每个可能取值又是2^n个bit,所以如果用穷举法来找到最优的w是不可行的,还是在求解一个w时,固定剩下的w不变。在求z时,此时$\alpha$和w是确定的,且此处将激活值量化函数条件放宽,在0~M范围内的数值就不进行量化,所以针对不同分布得到了z的求解方式。
对权重量化时,层与层之间可以同时进行,没有耦合关系,但是独立进行量化时,量化误差会在层与层之间累加,所以还是考虑通过按层量化。
TSQ通过稀疏量化激活值和引入一个中间变量z来产生新的量化方法,在alexnet上将权重激活值都量化到2bit时性能与浮点也是一致的。
LQ-Net
LQ-Net[13]目的是希望学习量化任意bit权重和激活值的quantizers,现有的量化方法都是一种人工设计的quantizers,例如均匀量化、对数量化,或者在网络训练之时已经计算好的quantizers(HGWQ),如果针对不同的网络能自适应的学到不同quantizers,性能应该会有所提升,所以本文就想联合训练一个量化的DNN网络和对应的quantizers。
$q_l$是量化levels,量化intervals指的是$t_l$到$t_{l+1}$,浮点值在$t_l$到$t_{l+1}$范围内的会被量化到$q_l$,均匀量化就是指每个$t_l$到$t_{l+1}$的范围都是相同的,对数量化是$t_l$到$t_{l+1}$的范围成指数关系,量化到n-bit,就有32/n或者64/n倍的压缩比例。但是由于每个卷积层的数据分布的不同,均匀量化不一定是最优的,预先设置好的量化方式也不一定是最优的,所以考虑既训练整个量化网络,也训练量化函数。如果量化函数是可以训练的,那么它不仅能够减少量化误差,也能适应整体的训练目标提升最终性能。
假设网络被量化到K-bit,一个整数q可以通过一个k维的basis系数向量v和k个bit的二值编码向量$e_l$点积表达,如公式14所示,此处的系数向量取值为整数。
$$
q=<\begin{bmatrix}
1\
2\\
…\
2^{K-1}\\
\end{bmatrix},
\begin{bmatrix}
b_1\\
b_2\
…\
b_K\\
\end{bmatrix}> \tag{14}
$$
由于二值编码向量$e_l$里面每个元素取值都是0和1,当k确定之后$e_l$所有取值可能都可以确定,例如K=2,$e_l$所有可能为{(-1,-1),(-1,1),(1,-1),(1,1)}。v是一个可学习的浮点basis系数向量,v值确定之后和每一组可能的二值编码向量相乘$q_l=v^Te_l$,得到了一系列的量化levels,量化intervals就是两个level之间的均值。
对权重和激活值都进行相同的量化操作,卷积就变成了$Q_{ours}(w,v^w)^TQ_{ours}(a,v^a)=\sum_{i=1}^{K_w}\sum_{j=1}^{K_a}v_i^wv_j^a(b_i^w\odot b_j^a)$,其中有两组要学习的参数,分别是$v_w$和$v_a$,同一层的激活值量化共用一个$v_a$向量,一层权重对应每个输出channel用一个$v_w$向量。
在量化和更新过程中,在训练开始之前通过一个经验公式求出初始的v,然后先固定v更新B,此时v是已知的,可以直接计算出所有levels,对比浮点数x落在哪个区间就量化到对应的B。然后固定B更新v,通过最小化量化误差$\underset{v,B}{argmax}||B^Tv-x||_2^2$对v求闭式解$v^*=(BB^T)^{-1}Bx$来更新当前的v。
LQ-Net算法通过学习得到量化levels,而不是人为设计的quantizers,可以量化到任意的bit,在几个开源数据集上都有非常不错的性能表现。
小结
写到后面,感觉意识有点模糊了,到现在我已经工作了一年多了,今年开始在做模型量化方面的工作,因为需要保护公司的利益,不可能在文章中聊工作的事情,所以只能分享了几篇个人觉得做这个方向需要了解的一些文章,如果有不足的地方,希望大家批评指正,谢谢了。
[1] Maxout Networks
[2] BinaryConnect: Training Deep Neural Networks with binary weights during propagations
[5] From Hashing to CNNs: Training Binary Weight Networks via Hashing
[6] Learning Accurate Low-Bit Deep Neural Networks with Stochastic Quantization
[8] TRAINED TERNARY QUANTIZATION
[9] DOREFA-NET: TRAINING LOW BITWIDTH CONVOLUTIONAL NEURAL NETWORKS WITH LOW BITWIDTH GRADIENTS
[10] TRAINING AND INFERENCE WITH INTEGERS IN DEEP NEURAL NETWORKS
[11] Deep Learning with Low Precision by Half-wave Gaussian Quantization
[12] Two-Step Quantization for Low-bit Neural Networks
[13] LQ-Nets: Learned Quantization for Highly Accurate and Compact Deep Neural Networks
[14] ImageNet Classification with Deep Convolutional Neural Networks
[15] XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks
[16] Fixed-point Factorized Networks
[17] INCREMENTAL NETWORK QUANTIZATION: TOWARDS LOSSLESS CNNS WITH LOW-PRECISION WEIGHTS
[18] DOREFA-NET: TRAINING LOW BITWIDTH CONVOLUTIONAL NEURAL NETWORKS WITH LOW BITWIDTH GRADIENTS
[19] Network Sketching: Exploiting Binary Structure in Deep CNNs
[20] Towards Effective Low-bitwidth Convolutional Neural Networks
[21] SYQ: Learning Symmetric Quantization For Efficient Deep Neural Networks
[22] Very deep convolutional networks for large-scale image recognition
[23] Towards Accurate Binary Convolutional Neural Network
[24] Deep residual learning for image recognition
[25] Estimating or Propagating Gradients Through Stochastic Neurons for Conditional Computation