Assignment 1 & 2

发表于 | 分类于 |
本文主要介绍我在实现陈天奇老师的深度学习系统课程课后作业的过程中的一些思考和解决方法。

【转载请注明出处】chenrudan.github.io

本文主要介绍我在实现陈天奇老师的深度学习系统课程课后作业的过程中的一些思考和解决方法，这个课虽然没有视频，但是ppt做的非常好，assignment中已经给出了答案，编写程序可以直接检查结果是否正确，值得一做。本文会结合一些课中的ppt来解释。

现在的深度学习系统在实现上分为用户使用的接口、系统设计、计算实现三个部分，如图1所示。我所理解的的这三个部分内容如下，实现用户接口实际上就是实现compute graph中的一个个结点，用户通过定义好计算图再执行，并且会将自动求导加入计算过程，为什么这么做通过assignment 1来解释，接着是实现如何优化计算图的内部结构以及执行计算图的操作，第三部分就是实现具体卷积、relu等的计算。

图1 深度学习系统架构(图片来源[1])

Assignment 1

内容描述:Reverse-mode Automatic Differentiation

要实现的就一个auto_diff.py文件，主要有Node、Variable、Op、Executor等类，node就是compute graph中的每一个结点，结点代表的是某种计算，它会记录输入是哪个node，并保存对输入的某个操作op，op就是具体的计算内容，variable本质是一个op，但它本身不代表任何东西，填入什么就是什么，executor通过自己的run函数来调用op的compute函数来计算这个op。

这个文件大部分内容都已经实现了，而我们要填入的内容主要是各个op的compute函数以及这个op对应的gradient函数，以及用来计算整个计算图梯度的graidents函数，和执行整个计算图的executor的run函数。

这个作业的核心问题就是第四课的内容–实现自动求导。反向传播算法根据链式法则能够计算出目标函数对神经网络每一个结点的梯度，自动求导要做的也是计算目标函数对计算图中每一个node的梯度，这里面就涉及到需要计算每一个op的输出对输入的导数，因此针对每一个op来实现一个gradient函数，先把梯度计算出来。

最开始在思考如何实现op的梯度时，没有体会到自动求导的用意，当对任何在实现梯度，返回值都是直接计算的数值结果，就跟compute函数的计算方式一样，如下面的代码实现点乘mul_op的梯度。

1
2
3
4
5
6
7
8
9
10
def compute(self, node, input_vals):
    """Given values of two input nodes, return result of element-wise multiplication."""
    """TODO: Your code here"""
    assert len(input_vals) == 2
    return input_vals[0]*input_vals[1]

def gradient(self, node, output_grad):
    """Given gradient of multiply node, return gradient contributions to each input."""
    """TODO: Your code here"""
    return [output_grad*node.inputs[1], output_grad*node.inputs[0]]

按照这种想法，当实现矩阵乘法时发现做不出来了，因为gradient函数的输入值是node和这个op输出的梯度，要计算的是对node的梯度，而不像compute函数一样有input_vals这样的numpy数组，从而可以直接调用numpy的库函数。

1
2
3
4
5
6
7
8
9
10
11
12
def compute(self, node, input_vals):
    """Given values of input nodes, return result of matrix multiplication."""
    """TODO: Your code here"""
    assert len(input_vals) == 2
    if node.matmul_attr_trans_A == False and node.matmul_attr_trans_B == False:
        return np.dot(input_vals[0], input_vals[1])
    elif node.matmul_attr_trans_A == True and node.matmul_attr_trans_B == False:
        return np.dot(np.transpose(input_vals[0]), input_vals[1])
    elif node.matmul_attr_trans_A == False and node.matmul_attr_trans_B == True:
        return np.dot(input_vals[0], np.transpose(input_vals[1]))
    else:
        return np.dot(np.transpose(input_vals[0]), np.transpose(input_vals[1]))

这里就说明了graident肯定不是要计算出一个数值，经过思考，这里的gradient的输出应该是一个node，而node本身又是有op，op是有compute函数的，所以自动求导的出发点是将梯度当成计算图中的node，没有所谓的前向后向，在执行时，只向前计算每一个node的compute函数。此处求解矩阵乘法的梯度是实现成了如下的方式。

1
2
3
4
5
6
7
8
def gradient(self, node, output_grad):
    """Given gradient of multiply node, return gradient contributions to each input.
        
    Useful formula: if Y=AB, then dA=dY B^T, dB=A^T dY
    """
    """TODO: Your code here"""
    return [matmul_op(output_grad, node.inputs[1], False, True),
            matmul_op(node.inputs[0], output_grad, True, False)]

那么接下来去实现executor的run函数就变得简单了，它只需按照node的顺序，一个个调用node中保存的op的compute函数，这个函数的每一步计算返回的都是数值，不是node。

1
2
3
4
5
6
7
8
for node in topo_order:

    if len(node.inputs) == 1:
        node_to_val_map[node] = node.op.compute(node, [node_to_val_map[node.inputs[0]]])
    elif len(node.inputs) == 2:
        node_to_val_map[node] = node.op.compute(node,
                                               [node_to_val_map[node.inputs[0]],
                                                node_to_val_map[node.inputs[1]]])

最后需要实现的是graidents函数，它的功能是求出给定的node列表的每一个成员的梯度，实际上做的事情就是将从输出到输入的所有node对应梯度按照依赖关系排列出梯度计算图，计算图与梯度计算图之间通过output结点的梯度由output结点大小决定而关联起来，如下图的红色node计算图，再针对给定的node列表进行返回。

图2 自动求导(图片来源[2])

基于课程中的自动求导的伪码可以得出下面求解gradients函数的实现。

1
2
3
4
5
6
7
8
9
10
11
12
for node in reverse_topo_order:

    #将输出多条线得到的grad加起来
    grad = sum_node_list(node_to_output_grads_list[node])
    node_to_output_grad[node] = grad
    input_grads = node.op.gradient(node, grad)

    for id in range(len(node.inputs)):
        if node.inputs[id] not in node_to_output_grads_list:
            node_to_output_grads_list[node.inputs[id]] = [input_grads[id]]
        else:
            node_to_output_grads_list[node.inputs[id]].append(input_grads[id])

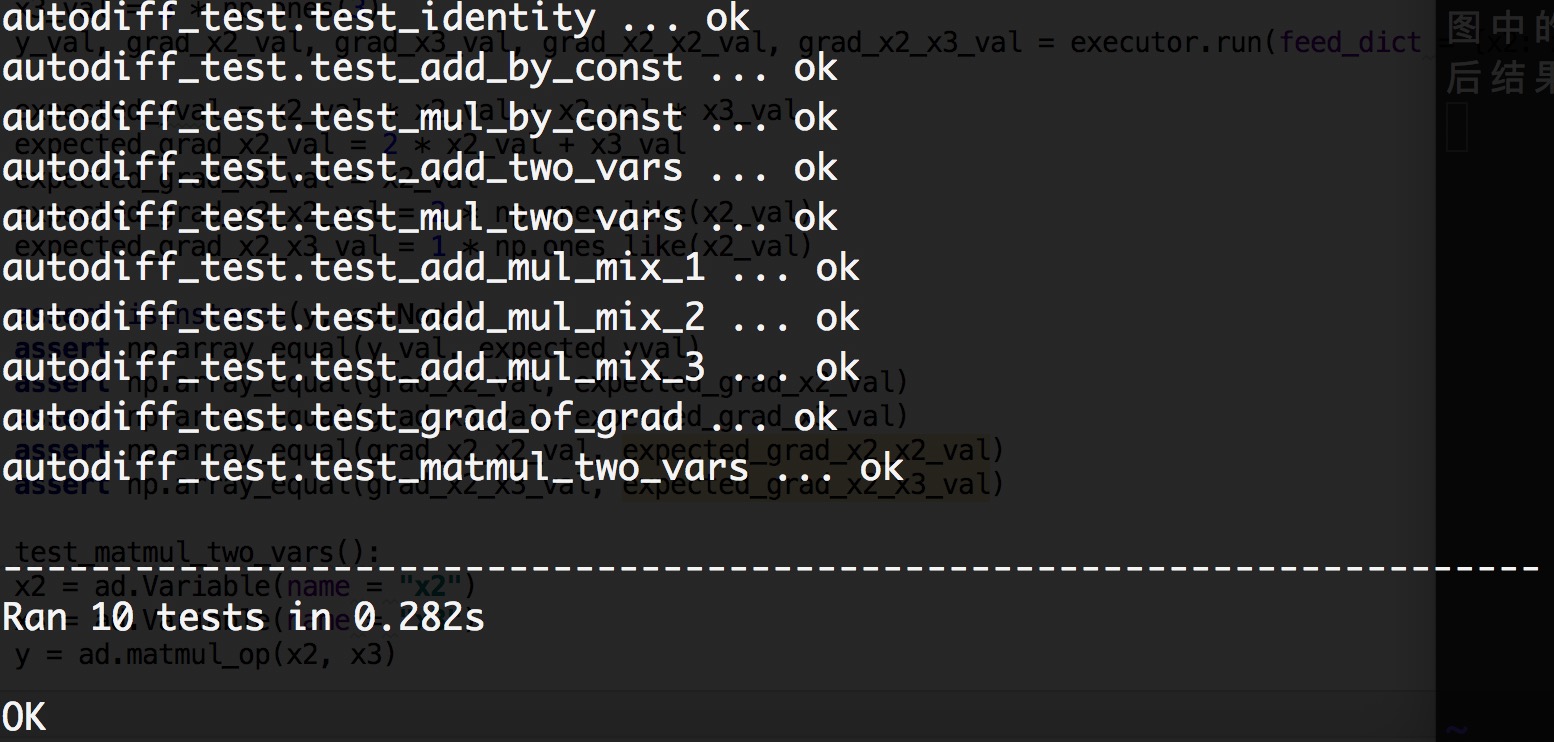
以上就是assignment1的一些内容和我的一些思考，我觉得最重要的想法就是将node的梯度也变成计算图中的一个node，这样就能很方便的实现自动求导，执行一遍计算图就将要求的东西全部求出来了。最后结果如下，如果代码有问题，会返回Error，如果代码执行错误，会返回Fail。

图3 assignment1结果

Assignment 2

内容描述：Assignment 2: GPU Graph Executor

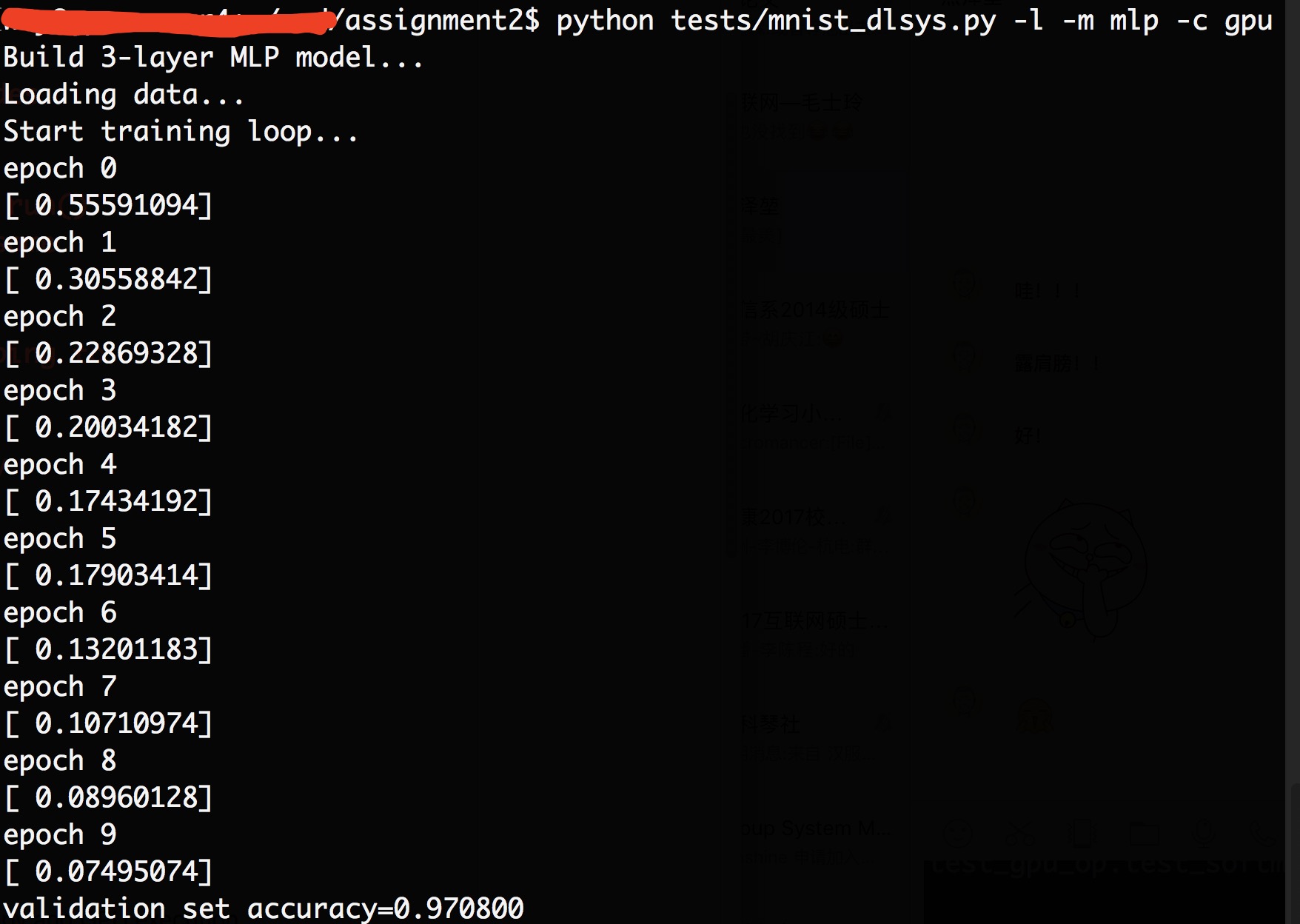
需要实现的主要有两个部分，一个是src/gpu_op.cu文件通过gpu现实op，一个是python/dlsys/autodiff.py实现优化内存。有两个测试方式，一种是tests/test_gpu_op.py只测试写的gpu代码正确性，一种是tests/mnist_dlsys.py会基于之前的所有代码实现一个逻辑回归和mlp看运行结果是否正确。

gpu这个部分没什么好说的，需要自己实现host函数和kernel函数，kernel函数的逻辑很简单，看过一些gpu教程之后肯定没问题，要注意的就是输入的维数在test_gpu_op.py和mnist_dlsys.py中可能不相等。还有使用cublas库的时候，这个库认为数据的存储方式是按列存储，所以在处理上我将输入的两个矩阵换了位置。课程给出的一段示例代码中有下面的形式，一个block中最大thread的个数是1024，threads.x取1024之后，threads.y不能再取大于1的值，所以这样的写法我觉得不太正确。

1
2
3
4
5
6
7
dim3 threads;
if (nrow <= 1024) {
  threads.x = nrow;
} else {
  threads.x = 1024;
  threads.y = (nrow + 1023) / 1024;
}

另外，在autodiff.py中需要实现内存优化，根据第七课的ppt，内存优化的出发点其实就是记录下已经给每个node分配的内存空间大小，并且不释放已经分配好的空间，如果后面node需要的内存大小跟前面的一样且前面的空间已经空闲，那么这块内存就能复用。

图4 内存优化算法(图片来源[3])

那么需要实现的就两个部分，一是记录下每个op的形状，用来确定需要的内存空间大小，实现的函数就是infer_shape，它有op的输入结点的形状数组，推断出这个op输出的形状数组，例如下面add_op对应的函数为:

1
2
3
4
5
6
7
   def infer_shape(self, node, input_shapes):
       """Need to handle input_vals[0].shape != input_vals[1].shape"""
       """TODO: Your code here"""
if input_shapes[0] == input_shapes[1]:
       	return input_shapes[0]
else:
	return input_shapes[1]

另外就是在已知每个node的形状数组情况下，决定内存如何进行复用，重点是要确定已分配的内存何时能够被重写，因为当内存a在作为内存b和c的输入时，就算内存b跟a大小一模一样，也不能直接将b写入a的内存空间，因为c还要用，因此我给出的解决方案如下，首先记录每个node它会被多少node使用，保存在num_of_output中，key是node，索引是这个node被作为输入的次数。用变量shapes_has_arise来保存出现过的形状数组，将形状数组作为key，value是已经分配了这个形状数组的node集合，变量memory_can_be_reuse保存每一个结点已经作为输入的次数，当作为输入的次数已经达到在num_of_output中存储的数字时说明这块内存已经可以被重新使用了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
shapes_has_arise = {}
self.node_to_arr_map = {}
num_of_output = {}
memory_can_be_reuse = {}
for node in self.topo_order:
	num_of_output[node] = 0
for node in self.topo_order:
	for input_node in node.inputs:
		num_of_output[input_node] += 1

for node in self.topo_order:
	if node not in feed_shapes:
	//如果内存形状没有出现过，就分配这块内存保存在node_to_arr_map中，并将这个结点记录在memory_can_be_reuse
	if str(self.node_to_shape_map[node]) not in shapes_has_arise:
		self.node_to_arr_map[node] = ndarray.empty(self.node_to_shape_map[node], ctx=self.ctx)
		shapes_has_arise[str(self.node_to_shape_map[node])] = [node]
		//这个结点不能被使用
		memory_can_be_reuse[node] = 0
					
	else:
		need_new_alloc = True
		//假如内存形状已经出现过，遍历已经分配了相同形状的node
		//如果这块内存被使用的次数已经到达记录的次数，那么就作为新的空间使用
		for i in range(len(shapes_has_arise[str(self.node_to_shape_map[node])])):
			allocated_node = shapes_has_arise[str(self.node_to_shape_map[node])][i]
			if memory_can_be_reuse[allocated_node] < num_of_output[allocated_node]:
				memory_can_be_reuse[allocated_node] += 1
			else:
				self.node_to_arr_map[node] = self.node_to_arr_map[allocated_node]
				need_new_alloc = False
				break
							
		if need_new_alloc:
			self.node_to_arr_map[node] = ndarray.empty(self.node_to_shape_map[node], ctx=self.ctx)
			shapes_has_arise[str(self.node_to_shape_map[node])].append(node)
			memory_can_be_reuse[node] = 0
		else:
			del shapes_has_arise[str(self.node_to_shape_map[node])][i]
			memory_can_be_reuse[node] = 0
			shapes_has_arise[str(self.node_to_shape_map[node])].append(node)

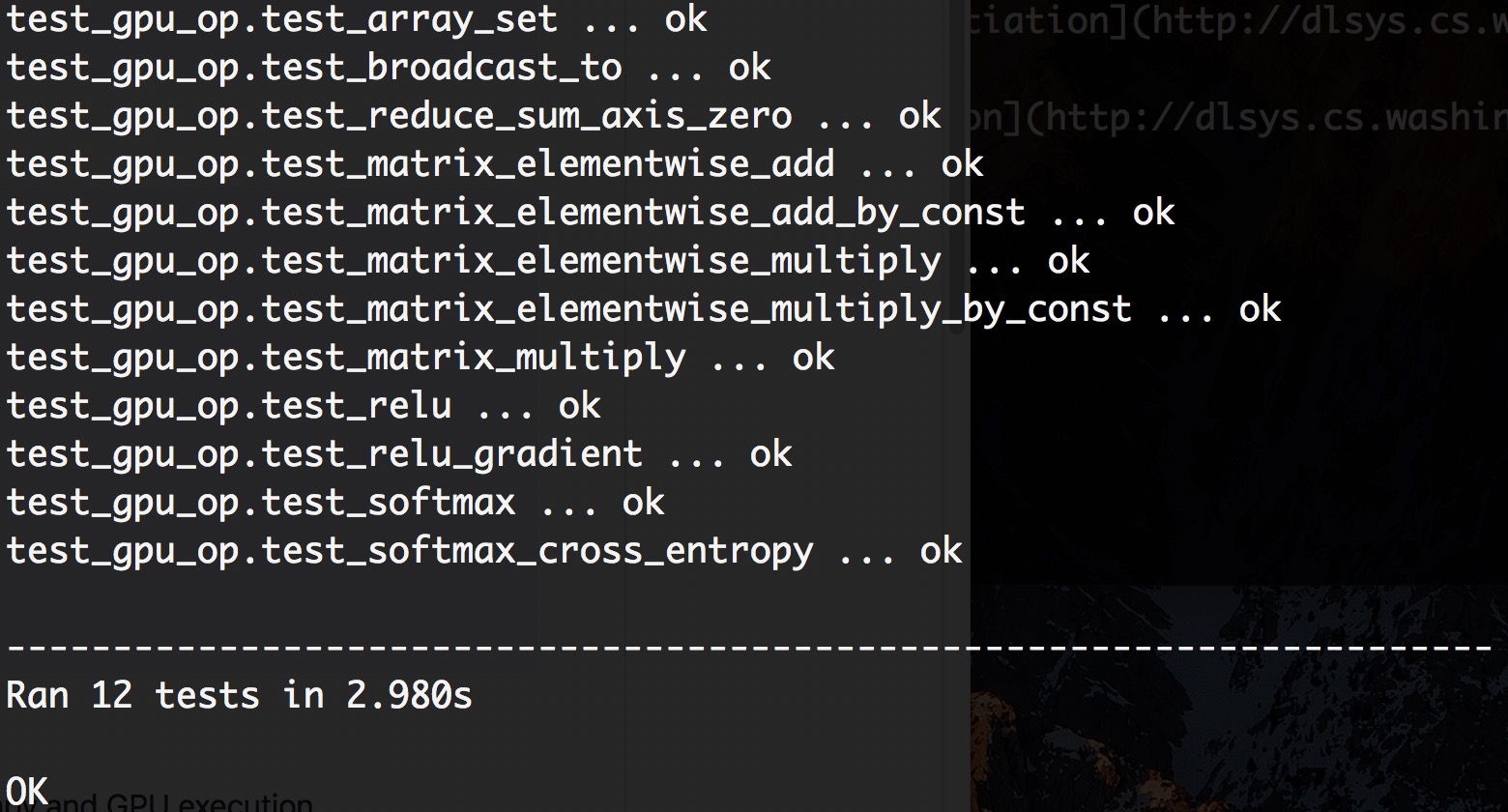
相应的结果输出如下:

图5 gpu程序输出结果

图6 mlp输出结果

引用：

[1] Lecture 3: Overview of Deep Learning System

[2] Lecture 4: Automatic Differentiation

[3] Lecture 7: Memory Optimization