【转载请注明出处】chenrudan.github.io
本文是David Silver强化学习公开课第四课的总结笔记。这一课主要讲了解决在未知environment的情况下强化学习的prediction问题的两种方法,分别是Monte-Carlo Reinforcement Learning和Temporal Difference。
本课视频地址:RL Course by David Silver - Lecture 4: Model-Free Prediction。
本课ppt地址:http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching_files/MC-TD.pdf。
文章的内容是课程的一个总结和讨论,会按照自己的理解来组织。个人知识不足再加上英语听力不是那么好可能会有一些理解不准的地方,欢迎一起讨论。
建了一个强化学习讨论qq群,有兴趣的可以加一下群号595176373或者扫描下面的二维码。

1.内容回顾
上节课中通过动态规划能够解决已知environment的MDP问题,也就是已知$S,A,P,R,\gamma$,其中根据是否已知policy将问题又划分成了prediction和control问题,本质上来说这种known MDP问题已知environment即转移矩阵与reward函数,但是很多问题中environment是未知的,不清楚做出了某个action之后会变到哪一个state也不知道这个action好还是不好,也就是说不清楚environment体现的model是什么,在这种情况下需要解决的prediction和control问题就是Model-free prediction和Model-free control。显然这种新的问题只能从与environment的交互得到的experience中获取信息。
这节课要解决的问题是Model-free prediction,即未知environment的Policy evaluation,在给定的policy下,每个state的value function是多少。
将从某个起始状态开始执行到终止状态的一次遍历$S_1,A_1,R_2,…,S_k$称为episode。已知很多的episodes。
2.Monte-Carlo Reinforcement Learning
蒙特卡洛强化学习是假设每个state的value function取值等于多个episodes的return $G_t$的平均值,它需要每个episode是完整的流程,即一定要执行到终止状态。由第二课中知道值函数的表达式为$v_{\pi}(s)=E_{\pi}[G_t|S_t=s]$,即每个state的value function是return的期望值,而在Monte-Carlo policy evaluation的假设下,值函数的取值从期望简化成了均值。
因此在本算法中,需要记录两个值,状态s被访问到的次数$N(s) = N(s)+1$以及每次访问时return之和$S(s) = S(s) + G_t$,遍历完所有的episodes之后,得到状态s下值函数取值为$V(s)=S(s)/N(s)$。而这里有两种访问次数的记录方式,一种是在一个episode中只记录第一次访问到的s,一种是一个episode中每次访问到s都记录下来。从而针对一次新的访问,先次数加1$N(S_t)=N(S_t)+1$,然后更新$V(S_t) = V(S_t)+\frac{1}{N(S_t)}(G_t-V(S_t))$。在一些方法中也会将$\frac{1}{N(S_t)}$设置成一个常数$\alpha$,不随着访问次数增加,即
$$
V(S_t) = V(S_t)+\alpha(G_t-V(S_t))::::(1)
$$
3.Temporal-Difference Learning
时序差分学习则是基于Bootstrapping思想,即在中间状态中会估计当前可能获得的return,并且更新之前状态能获得的return。因此它不需要走完一个episode的全部流程才能获得return。在最简单的TD算法TD(0)中这个估计return为$R_{t+1}+\gamma V(S_{t+1})$称之为TD target,代入上面公式2替代掉$G_t$就能得到TD算法的value function更新公式。
$$
V(S_t) = V(S_t)+\alpha(R_{t+1}+\gamma V(S_{t+1})-V(S_t))::::(2)
$$
$\delta_t = R_{t+1}+\gamma V(S_{t+1})-V(S_t)$称之为TD error。它代表了估计之前和估计之后的return差值。
TD(0)是指在某个状态s下执行某个动作后转移到下一个状态$s’$时,估计$s’$的return再更新s,假如s之后执行两次动作转移到$s’’$时再反回来更新s的值函数,那么就是另一种形式,从而根据step的长度n可以扩展TD到不同的形式,当step长度到达当前episode终点时就变成了MC。从而得到统一公式如下
$$
G_t^{(n)} = R_{t+1} + \gamma R_{t+2} + … + \gamma ^{n-1}R_{t+n}+\gamma ^nV(S_{t+n}) :::: (3)
$$
$$
V(S_t) = V(S_t) + \alpha(G_t^{(n)} - V(S_t)) ::::(4)
$$
又如果将不同的n对应的return平均一下,这样能够获得更加robust的结果,而为了有效的将不同return合起来,对每个n的return都赋了一个权重$1-\lambda, (1-\lambda)\lambda,…,(1-\lambda)\lambda^n$,参数是$\lambda$,这样又能得到一组更新value function的公式。
$$
G_t^{\lambda} = (1-\lambda)\sum_{n=1}^{\infty }\lambda^{n-1}G_t^{(n)} :::: (5)
$$
$$
V(S_t) = V(S_t) + \alpha(G_t^{\lambda} - V(S_t)) ::::(6)
$$
下面左图是一个从办公室驾驶回家的路上花费时间的例子,第一列表示当前状态,例如下雨,离开高速等等,第二列表示当前花费时间,第三列表示估计还有多久能到家,第四列是前两列之和,表示估计要花费的总时间。要求的value function是当前状态下要到家的总时间,针对这个问题,MC和TD算法都给出了自己的解决结果,即右图中的虚线。可以明显看出来蒙特卡洛方法是根据整个流程走完了之后,根据最后的结果更新了前面每个state的value function都是43,而TD则是走完一步,发现当前花费总时间发生了变化,就更新上一个状态所需的时间,因此第一个状态的value function取值是40,第二个状态value function取值是35等等。
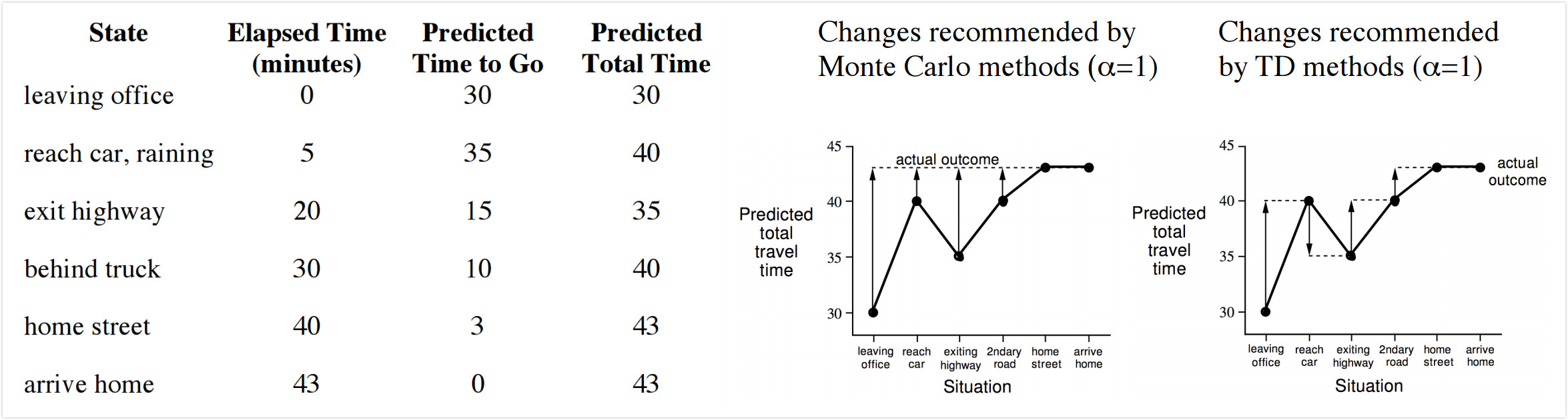
4.Monte-Carlo VS. Temporal Difference
在谈两种算法的优劣前,先谈谈Bias/Variance tradeoff的问题。平衡Bias/Variance是机器学习比较经典的一个问题,bias是指预测结果与真实结果的差值,variance是指训练集每次预测结果之间的差值,bias过大会导致欠拟合它衡量了模型是否准确,variance过大会导致过拟合衡量了模型是否稳定。如果$G_t$和$R_{t+1}+\gamma v_{\pi}(S_{t+1})$跟真实值一样,那么就是无偏差估计。因为在MC算法中,它是将最终获得的reward返回到了前面的状态,因此是真实值,但是它采样的episode并不能代表所有的情况,所以会导致比较大的variance。而TD的$R_{t+1}+\gamma V(S_{t+1})$跟真实值是有偏差的,在计算的过程基于随机的状态、转移概率、reward等等,涵盖了一些随机的采样,因此variance比较小。
此外,MC方法中没有计算状态转移概率,也不考虑状态转移,它的目标是最小化均方误差,这样的行为实际上并不符合马尔可夫性质,而TD方法会找出拟合数据转移概率和reward函数,还是在解决MDP问题。
| Monte-Carlo | Temporal Difference |
|---|---|
| 要等到episode结束才能获得return | 每一步执行完都能获得一个return |
| 只能使用完整的episode | 可以使用不完整的episode |
| 高variance,零bias | 低variance,有bias |
| 没有体现出马尔可夫性质 | 体现出了马尔可夫性质 |
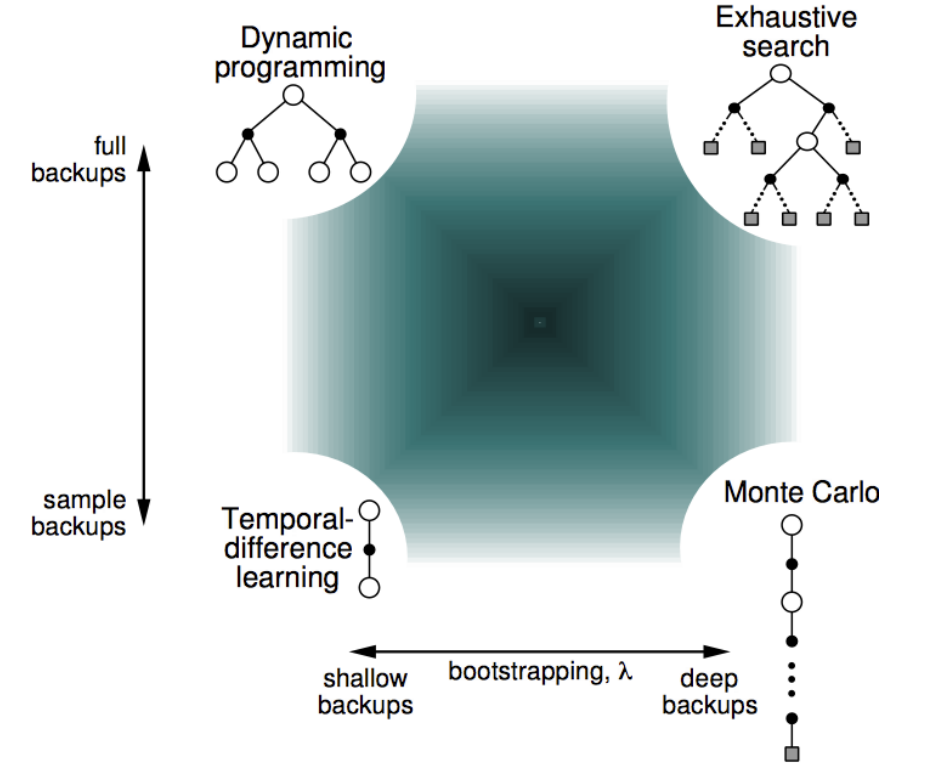
上面的图是用Policy Evaluation解决强化学习问题的一些算法的区别与相关性,最左边的竖线表示如果考虑了所有的可能发生的情况那么就是动态规划,如果只考虑了部分采样那么就是时序差分。下面的横线表示如果考虑了一次episode中全部的动作就是Monte-Carlo,如果只考虑部分动作就是时序差分。如果又考虑全部情况又考虑每一种情况的全部动作就是穷举。
[1] http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching_files/MC-TD.pdf。