【转载请注明出处】chenrudan.github.io
本文是David Silver强化学习公开课第三课的总结笔记。主要谈到了动态规划能够解决MDP的什么问题,能通过Policy Iteration和Value Iteration来解决,这两者指的是什么,出于什么样的考虑提出这两种思路,具体解决步骤是什么。
本课视频地址:RL Course by David Silver - Lecture 3: Planning by Dynamic Programming。
本课ppt地址:http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching_files/DP.pdf。
文章的内容是课程的一个总结和讨论,会按照自己的理解来组织。个人知识不足再加上英语听力不是那么好可能会有一些理解不准的地方,欢迎一起讨论。
建了一个强化学习讨论qq群,有兴趣的可以加一下群号595176373或者扫描下面的二维码。

1.内容回顾
前两节课我忽略了一些内容,这节课用到了,所以先回顾一下。首先是Planning的概念,在第一节课提到过强化学习是一种Sequential Decision Making问题,它是一种试错(trial-and-error)的学习方式,一开始不清楚environment的工作方式,不清楚执行什么样的行为是对的,什么样是错的,因而agent需要从不断尝试的经验中发现一个好的policy。而Planning也属于Sequential Decision Making问题,不同的是它的environment是已知的,例如游戏的规则是已知的,所以agent不需要通过与environment的交互来获取下一个状态,而是知道自己执行某个action之后状态是什么,再优化自己的policy。因此这两者之间是有联系的,假如强化学习学习出来environment的模型,知道了environment是如何work的,强化学习要解决的问题就是Planning了。
在第二课中,推导出了几个Bellman方程,回顾一下。
| Bellman方程 | 形式 |
|---|---|
| Bellman Expectation Equation | $v_{\pi}(s) = \sum_{a\in A}\pi(a\s)q_{\pi}(s,a) =\sum_{a\in A}\pi(a\s)(R_s^a + \gamma \sum_{s’\in S}P_{ss’}^av_{\pi}(s’))$ |
| Bellman Expectation Equation | $q_{\pi}(s,a) = R_s^{a} + \gamma \sum_{s’ \in S}P_{ss’}^av_\pi(s’)=R_s^a + \gamma \sum_{s’\in S}P_{ss’}^a\sum_{a’\in A}\pi(a’\s’)q_{\pi}(s’,a’)$ |
| Bellman Optimality Equation | $v_*(s) = \underset{a}{max}q_*(s,a) = \underset{a}{max} R_s^{a} + \gamma \sum_{s’ \in S}P_{ss’}^av_*(s’)$ |
| Bellman Optimality Equation | $q^*(s,a) = R_s^{a} + \gamma \sum_{s’ \in S}P_{ss’}^av_*(s’) = R_s^a + \gamma \sum_{s’\in S}P_{ss’}^a \underset{a’} {max}q^*(s’, a’)$ |
2. 动态规划与Planning
动态规划是这样一种方法,它将一个复杂的问题切分成一系列简单的子问题,一旦解决了这些简单的子问题,再将这些子问题的解结合起来变成复杂问题的解,同时将它们的解保存起来,如果下一次遇到了相同的子问题那么就不用再重新计算子问题的解[1]。其中“动态”是指某个问题是由序列化状态组成,状态step-by-step的改变,从而可以step-by-step的来解这个问题,“规划”即优化子问题。而MDP有Bellman方程能够被递归的切分成子问题,同时它有值函数,保存了每一个子问题的解,因此它能通过动态规划来求解。针对MDP,切分成的子问题就是在每个状态下应该选择的action是什么,MDP的子问题是以一种递归的方式存在,这一时刻的子问题取决于上一时刻的子问题选择了哪个action。
MDP需要解决的问题有两种,第一种是prediction,它已知MDP的$S,A,P,R,\gamma$以及policy,目标是算出在每个状态下的value function,即处于每个状态下能够获得的reward是多少。而第二种是control,它已知MDP的$S,A,P,R,\gamma$但是policy未知,因此它的目标不仅是计算出最优的value function而且要给出最优的Policy。
当已知MDP的状态转移矩阵时,environment的模型就已知了,此时可以看成Planning问题,动态规划则是用来解决MDP的Planning问题,主要解决途径有两种,Policy Iteration和Value Iteration。
3. Policy Iteration
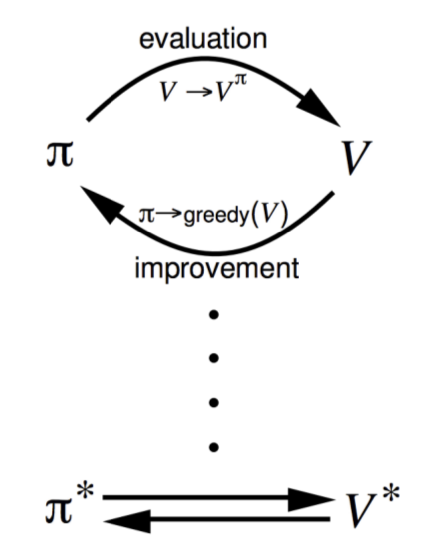
这个解决途径主要分为两步,示意图见图1:
- Policy Evaluation:基于当前的Policy计算出每个状态的value function
- Policy Improvment:基于当前的value function,采用贪心算法来找到当前最优的Policy
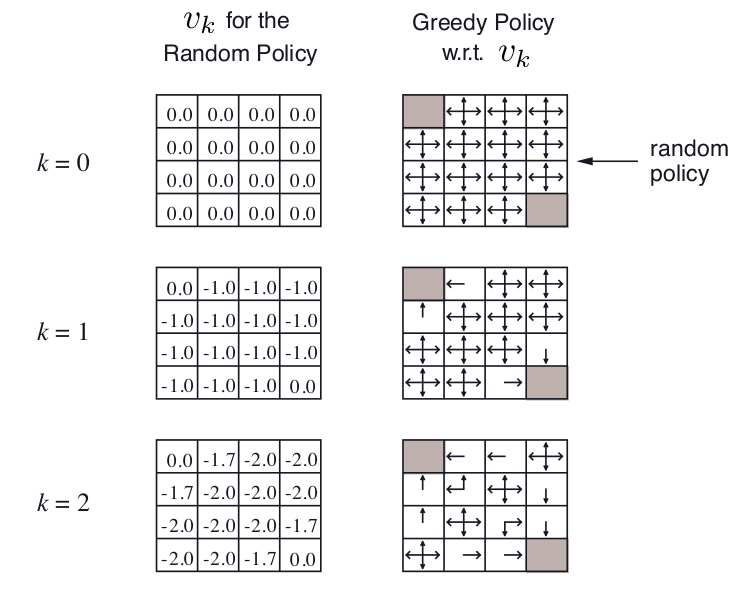
这里的Policy Evaluation要求的$v(s)$是通过计算第一个Bellman Expectation Equation得到的。下图是一个叫Small Gridworld的例子,左上角和右下角是终点,$\gamma = 1$,移动一步reward减少1,起始的random policy是朝每个能走的方向概率相同,先单独看左边一列,它表示在第k次迭代每个state上value function的值,这一列始终采用了random policy,这里的value function就是通过Bellman Expectation Equation得到的,考虑k=2的情况,-1.7 = -1.0 + 2*(1/3.0)*(-1),-2.0 = -1.0 + 4*(1/4.0)*(-1)。而右边一列就是在当前的value function情况下通过greedy算法找到当前朝哪个方向走更好。
Policy Iteration会一直迭代到收敛,具体证明过程可以去看视频(46:09起)。
3. Value Iteration
最优化原理:当且仅当任何从s能达到的$s’$能在当前policy下获取最优的value即$v_{\pi}(s’) = v_{*}(s’)$,那么状态s也能在当前policy下获得最优value$v_{\pi}(s) = v_{*}(s)$。
从上面原理出发,如果已知子问题的最优值$v_{*}s’$,那么就能通过第一个Bellman Optimality Equation将$v_{*}(s)$也推出来。因此从终点开始向起点推就能把全部状态最优值推出来。Value Iteration通过迭代的方法,通过这一步的$v_k(s’)$更新下一步的$v_{k+1}(s)$不断迭代,最终收敛到最优的$v_{*}$,需要注意的是中间生成的value function的值不对应着任何policy。
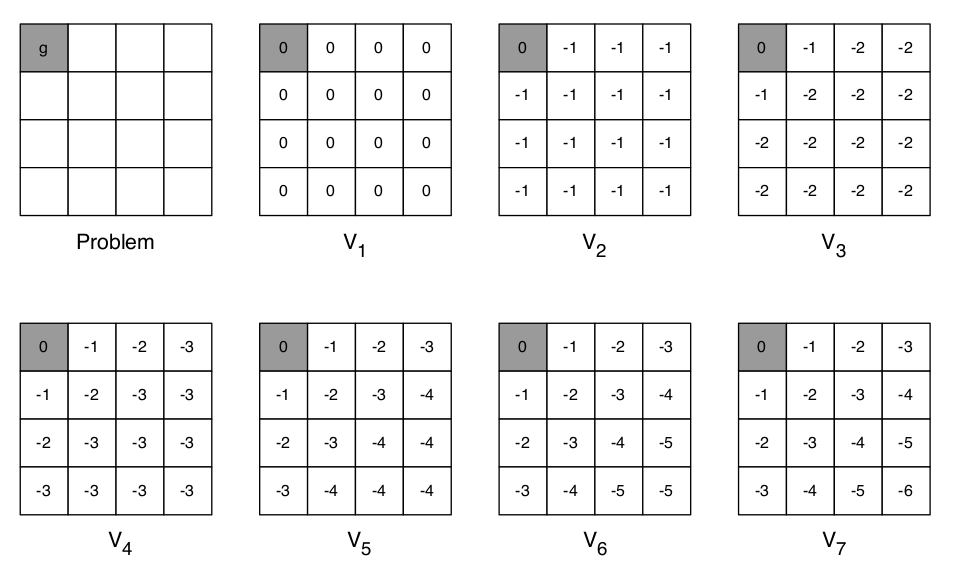
考虑下面这个Shortest Path例子,左上角是终点,要求的是剩下每一个格子距离终点的最短距离,每走一步,reward减少1,根据Value Iteration计算Bellman Optimality Equation就能得到后面的每一个正方形格子取值。
因此,针对MDP要解决的两个问题,有如下几种方式来解决。针对prediction,因为它的目标是在已知的Policy下得到收敛的value function,因此针对问题不断迭代计算Bellman Expectation Equation就够了,但是control则需要同时获得最优的policy,那么在Iterative Policy Evaluation的基础上加入一个选择Policy的过程就行了,也就是上面的Policy Iteration,另外Value Iteration虽然在迭代的过程中没有显式计算出policy,但是在得到最优的value function之后就能推导出最优的policy,因此也能用做解决control问题。
| 问题 | 使用到的Bellman Equation | 解决算法 |
|---|---|---|
| Prediction | Bellman Expectation Equation | Iterative Policy Evaluation |
| Control | Bellman Expectation Equation + Greedy Policy Improvement | Policy Iteration |
| control | Bellman Optimality Equation | Value Iteration |
以上是本课主要内容,后面还提了一下异步动态规划,并且提到了以上动态规划的解法适合状态个数百万级别的问题。总之,这节课需要搞懂的问题是动态规划能解决什么样的MDP问题以及具体怎样通过Policy Iteration和Value Iteration做到的。