简述生成式对抗网络

【转载请注明出处】chenrudan.github.io

本文主要阐述了对生成式对抗网络的理解，首先谈到了什么是对抗样本，以及它与对抗网络的关系，然后解释了对抗网络的每个组成部分，再结合算法流程和代码实现来解释具体是如何实现并执行这个算法的，最后给出一个基于对抗网络改写的去噪网络运行的结果，效果虽然挺差的，但是有些地方还是挺有意思的。

1. 对抗样本
2. 生成式对抗网络GAN
3. 代码解释
4. 运行实例
5. 小结
6. 引用

1. 对抗样本(adversarial examples)

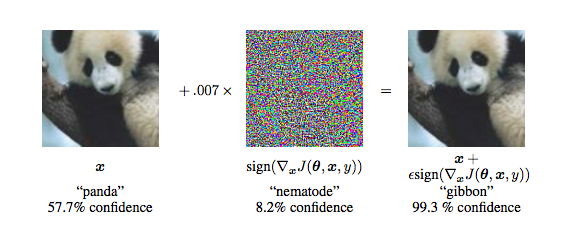
14年的时候Szegedy在研究神经网络的性质时，发现针对一个已经训练好的分类模型，将训练集中样本做一些细微的改变会导致模型给出一个错误的分类结果，这种虽然发生扰动但是人眼可能识别不出来，并且会导致误分类的样本被称为对抗样本，他们利用这样的样本发明了对抗训练(adversarial training)，模型既训练正常的样本也训练这种自己造的对抗样本，从而改进模型的泛化能力[1]。如下图所示，在未加扰动之前，模型认为输入图片有57.7%的概率为熊猫，但是加了之后，人眼看着好像没有发生改变，但是模型却认为有99.3%的可能是长臂猿。

图1 对抗样本的产生(图来源[2])

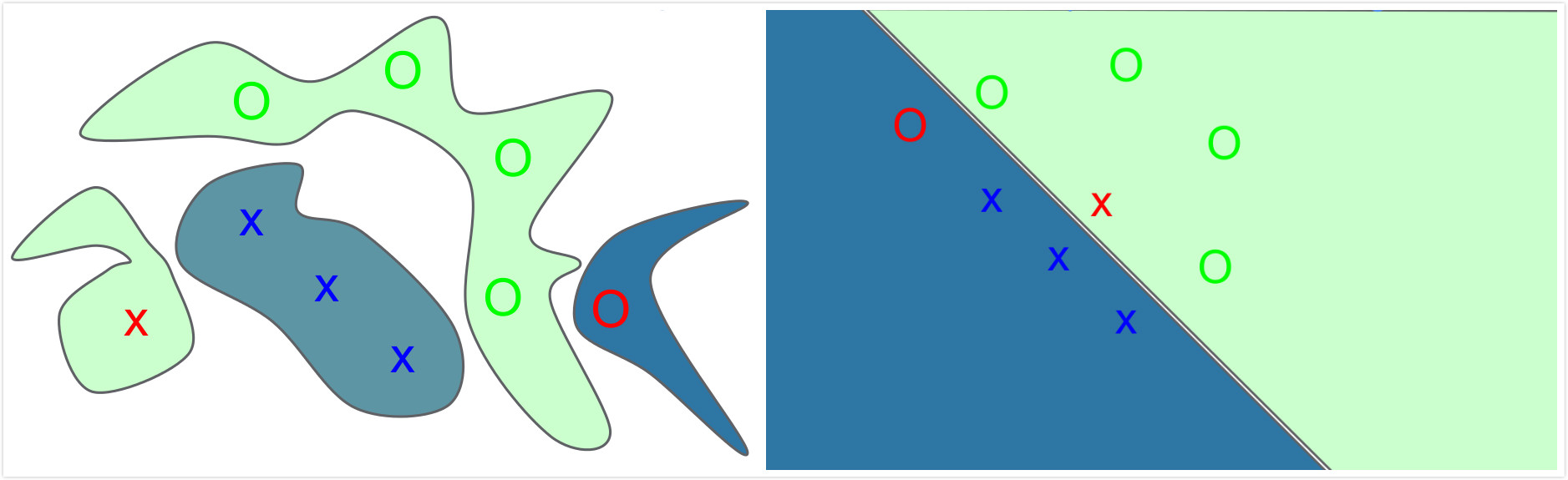
这个问题乍一看很像过拟合，在Goodfellow在15年[3]提到了其实模型欠拟合也能导致对抗样本，因为从现象上来说是输入发生了一定程度的改变就导致了输出的不正确，例如下图一，上下分别是过拟合和欠拟合导致的对抗样本，其中绿色的o和x代表训练集，红色的o和x即对抗样本，明显可以看到欠拟合的情况下输入发生改变也会导致分类不正确(其实这里我觉得有点奇怪，因为图中所描述的对抗样本不一定就是跟原始样本是同分布的，感觉是人为造的一个东西，而不是真实数据的反馈)。在[1]中作者觉得这种现象可能是因为神经网络的非线性和过拟合导致的，但Goodfellow却给出了更为准确的解释，即对抗样本误分类是因为模型的线性性质导致的，说白了就是因为$w^Tx$存在点乘，当$x$的每一个维度上都发生改变$\widetilde{x}=x+\eta$，就会累加起来在点乘的结果上附加上一个比较大的和$w^T\widetilde{x} = w^Tx+w^T\eta $，而这个值可能就改变了预测结果。例如[4]中给出的一个例子，假设现在用逻辑回归做二分类，输入向量是$x = [2, -1, 3, -2, 2, 2, 1, -4, 5, 1]$，权重向量是$w = [-1, -1, 1, -1, 1, -1, 1, 1, -1, 1]$，点乘结果是-3，类预测为1的概率为0.0474，假如将输入变为$xad = x + 0.5w = [1.5, -1.5, 3.5, -2.5, 2.5, 1.5, 1.5, -3.5, 4.5, 1.5]$，那么类预测为1的概率就变成了0.88，就因为输入在每个维度上的改变，导致了前后的结果不一致。

图2 过/欠拟合导致对抗样本(图来源[3])

如果认为对抗样本是因为模型的线性性质导致的，那么是否能够构造出一个方法来生成对抗样本，即如何在输入上加扰动，Goodfellow给出了一种构造方法fast gradient sign method[2]，其中$J$是损失函数，再对输入$x$求导，$\theta$是模型参数，$\epsilon$是一个非常小的实数。图1中就是$\epsilon=0.007$。

$$
\eta = \epsilon sign(\triangledown_{x}J(\theta,x,y)) :::::(1)
$$

这个构造方法在[4]中有比较多的实例，这里截取了两个例子来说明，用imagenet图片缩放到64*64来训练一个一层的感知机，输入是64*64*3，输出是1000，权重是64*64*3*1000，训练好之后取权重矩阵对应某个输出类别的一行64*64*3，将这行还原成64*64图片显示为下图中第二列，再用公式1的方法从第一列的原始图片中算出第三列的对抗样本，可以看到第一行从预测为狐狸变成了预测为金鱼，第二行变成了预测为校车。

图3 构造对抗样本(图来源[4])

实际上不是只有纯线性模型才会出现这种情况，卷积网络的卷积其实就是线性操作，因此也有预测不稳定的情况，relu/maxout甚至sigmoid的中间部分其实也算是线性操作。因为可以自己构造对抗样本，那么就能应用这个性质来训练模型，让模型泛化能力更强。因而[2]给定了一种新的目标函数也就是下面的式子，相当于对输入加入一些干扰，并且也通过实验结果证实了训练出来的模型更加能够抵抗对抗样本的影响。

$$
\widetilde{J}(\theta,x,y) = \alpha J(\theta,x,y)+(1-\alpha)J(\theta,x+\epsilon sign(\triangledown_{x}J(\theta,x,y))) :::::(2)
$$

对抗样本跟生成式对抗网络没有直接的关系，对抗网络是想学样本的内在表达从而能够生成新的样本，但是有对抗样本的存在在一定程度上说明了模型并没有学习到数据的一些内部表达或者分布，而可能是学习到一些特定的模式足够完成分类或者回归的目标而已。公式1的构造方法只是在梯度方向上做了一点非常小的变化，但是模型就无法正确的分类。此外还观察到一个现象，用不同结构的多个分类器来学习相同数据，往往会将相同的对抗样本误分到相同的类中，这个现象看上去是所有的分类器都被相同的变化所干扰了。

2. 生成式对抗网络GAN

14年Goodfellow提出Generative adversarial nets即生成式对抗网络[5]，它要解决的问题是如何从训练样本中学习出新样本，训练样本是图片就生成新图片，训练样本是文章就输出新文章等等。如果能够知道训练样本的分布$p(x)$，那么就可以在分布中随机采样得到新样本，大部分的生成式模型都采用这种思路，GAN则是在学习从随机变量$z$到训练样本$x$的映射关系，其中随机变量可以选择服从正太分布，那么就能得到一个由多层感知机组成的生成网络$G(z;\theta_g)$，网络的输入是一个一维的随机变量，输出是一张图片。如何让输出的伪造图片看起来像训练样本，Goodfellow采用了这样一种方法，在生成网络后面接上一个多层感知机组成的判别网络$D(x;\theta_d)$，这个网络的输入是随机选择一张真实样本或者生成网络的输出，输出是输入图片来自于真实样本$p_{data}$或者生成网络$p_g$的概率，当判别网络能够很好的分辨出输入是不是真实样本时，也能通过梯度的方式说明什么样的输入更加像真实样本，从而通过这个信息来调整生成网络。从而$G$需要尽可能的让自己的输出像真实样本，而$D$则尽可能的将不是真实样本的情况分辨出来。下图左边是GAN算法的概率解释，右边是模型构成。

图4 GAN算法框图(图来源[6])

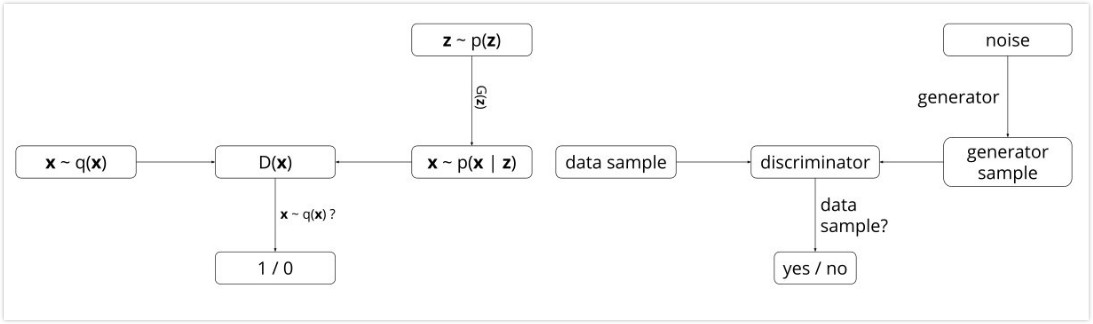
GAN的优化是一个极小极大博弈问题，最终的目的是generator的输出给discriminator时很难判断是真实or伪造的，即极大化$D$的判断能力，极小化将$G$的输出判断为伪造的概率，公式如下。论文[5]中将下面式子转化成了Jensen-shannon散度的形式证明了仅当$p_g=p_{data}$时能得到全局最小值，即生成网络能完全的还原出真实样本分布，并且证明了下式能够收敛。(算法流程论文讲的很清楚，这里就不说了，后面结合代码一起解释。)

$$
\underset{G}{min} : \underset{D}{max}V(D,G) =E_{x\sim p_{data}(x)}[logD(x)]+E_{z\sim p_{z}(z)}[log(1-D(G(z)))] :::::(3)
$$

以上是关于最基本GAN的介绍，最开始我看了论文后产生了几个疑问，1.为什么不能直接学习$G$，即直接学习一个$z$到一个$x$？2.$G$具体是如何训练的？3.在训练的时候$z$跟$x$是一一对应关系吗？在对代码理解之后大概能够给出一个解释。

3. 代码解释

这部分主要结合tensorflow实现代码[7]、算法流程和下面的变化图[5]解释一下具体如何使用DCGAN来生成手写体图片。

下图中黑色虚线是真实数据的高斯分布，绿色的线是生成网络学习到的伪造分布，蓝色的线是判别网络判定为真实图片的概率，标x的横线代表服从高斯分布x的采样空间，标z的横线代表服从均匀分布z的采样空间。可以看出$G$就是学习了从z的空间到x的空间的映射关系。

图5 GAN运行时各个概率分布图(图来源[5])

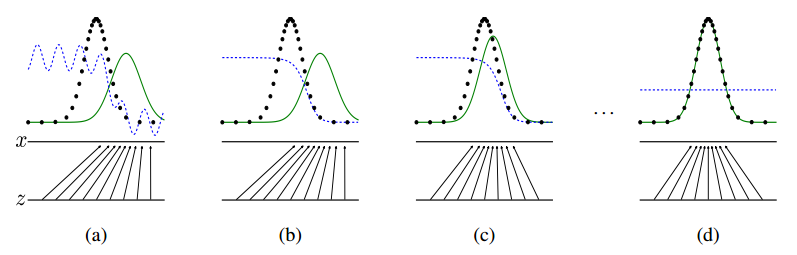
a.起始情况

$D$是一个卷积神经网络，变量名是D，其中一层构造方式如下。

w = tf.get_variable('w', [4, 4, c_dim, num_filter], 
initializer=tf.truncated_normal_initializer(stddev=stddev))
dconv = tf.nn.conv2d(ddata, w, strides=[1, 2, 2, 1], padding='SAME')
biases = tf.get_variable('biases', [num_filter], 
        initializer=tf.constant_initializer(0.0))
bias = tf.nn.bias_add(dconv, biases)
dconv1 = tf.maximum(bias, leak*bias)
...

$G$是一个逆卷积神经网络，变量名是G，其中一层构造方式如下。

w = tf.get_variable('w', [4, 4, num_filter, num_filter*2], 
        initializer=tf.random_normal_initializer(stddev=stddev))
deconv = tf.nn.conv2d_transpose(gconv2, w, 
        output_shape=[batch_size, s2, s2, num_filter], 
        strides=[1, 2, 2, 1])
biases = tf.get_variable('biases', [num_filter],
initializer=tf.constant_initializer(0.0))
bias = tf.nn.bias_add(deconv, biases)
deconv1 = tf.nn.relu(bias, name=scope.name)
...

$G$的网络输入为一个$z_{dim}$维服从-1~1均匀分布的随机变量，这里取的是100.

1 2	batch_z = np.random.uniform(-1, 1, [config.batch_size, self.z_dim]) .astype(np.float32)

$D$的网络输入是一个batch的64*64的图片，既可以是手写体数据也可以是$G$的一个batch的输出。

这个过程可以参考上图的a状态，判别曲线处于不够稳定的状态，两个网络都还没训练好。

b.训练判别网络

判别网络的损失函数由两部分组成，一部分是真实数据判别为1的损失，一部分是$G$的输出self.G判别为0的损失，需要优化的损失函数定义如下。

self.G = self.generator(self.z)
self.D, self.D_logits = self.discriminator(self.images)
self.D_, self.D_logits_ = self.discriminator(self.G, reuse=True)

self.d_loss_real = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(
            self.D_logits, tf.ones_like(self.D)))
self.d_loss_fake = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(
            self.D_logits_, tf.zeros_like(self.D_)))
self.d_loss = self.d_loss_real + self.d_loss_fake

然后将一个batch的真实数据batch_images，和随机变量batch_z当做输入，执行session更新$D$的参数。

# update discriminator on real
d_optim = tf.train.AdamOptimizer(FLAGS.learning_rate, 
        beta1=FLAGS.beta1).minimize(d_loss, var_list=d_vars)
...
out1 = sess.run([d_optim], feed_dict={real_images: batch_images, 
        noise_images: batch_z})

这一步可以对比图b，判别曲线渐渐趋于平稳。

c.训练生成网络

生成网络并没有一个独立的目标函数，它更新网络的梯度来源是判别网络对伪造图片求的梯度，并且是在设定伪造图片的label是1的情况下，保持判别网络不变，那么判别网络对伪造图片的梯度就是向着真实图片变化的方向。

1 2	self.g_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits( self.D_logits_, tf.ones_like(self.D_)))

然后用同样的随机变量batch_z当做输入更新

g_optim = tf.train.AdamOptimizer(config.learning_rate, beta1=config.beta1) 
            .minimize(self.g_loss, var_list=self.g_vars)
...
out2 = sess.run([g_optim], feed_dict={noise_images:batch_z})

这一步可以对比图c，$p_g$的曲线在渐渐的向真实分布靠拢。而网络训练完成之后可以看到$p_g$的曲线与$p_{data}$重叠在了一起，并且此时判别网络已经难以区分真实与伪造，因此取值就固定在了$\frac{1}{2}$。

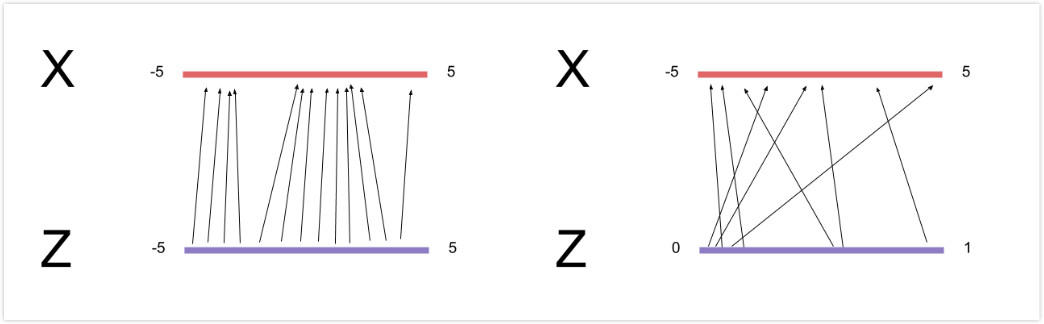
因而针对我之前的问题，2已经有了答案，针对1，为什么不能直接学习$G$?这是因为无法确定$z$与$x$的一一对应关系，就像下图，两种对应关系，如果要肯定谁是对谁是错，那么就得加入一些先验信息，甚至是直接对真实样本的估计，那么跟其他的方法不就一样了么。而问题3，在训练的时候$z$跟$x$是一一对应关系吗?我开始考虑这个问题是因为不清楚是不是一个100维的noise变量就对应着一个手写体变量图片，但是现在考虑一下就应该明白在训练的层面上不是一一对应的，甚至两者在训练$D$的时候都是分开的，只是可能在分布中会存在这样一种对应关系而已。

图6 z与x映射图(图来源[8])

4. 运行实例

这里本来想用GAN来跑一个去噪的网络，基于[7]的代码改了一下输入，从一个100维的noise向量变成了一张输入图片，同时将generator网络的前面部分变成了卷积网络，再连上原来的逆卷积，就成了一个去噪网络，这里我没太多时间来细致的调节网络层数、参数等，就随便试了一下，效果也不是特别的好。代码在[9]中。首先我通过read_stl10.py对stl10数据集加上了均值为0方差为50的高斯噪声，前后对比如下。

图7 增加高斯噪声前后对比

然后执行对抗网络，会得到如下的去噪效果，从左到右分别是加了噪声的输入图片，对应的generator网络的输出图片，已经对应的干净图片，效果不是特别好，轮廓倒是能学到一点，但是这个颜色却没学到。

图8 去噪对比

5. 小结

刚开始搜资料的时候发现了对抗样本，以为跟对抗网络有关系，就看了一下，后来看Goodfellow的论文时发现其实没什么关系，但是还是写了一些内容，因为这个东西的存在还是值得了解的，而对抗网络这个想法真的太赞了，它将一个无监督问题转化为有监督，更加像一种learn的方式来学习数据应该是如何产生，而不是find的方式来找某些特征，但是训练也是一个难题，从我的经验来看，特别容易过拟合，而且确实有一种对抗的感觉在里面，因为generator的输入时好时坏，总的来说是个很棒的算法，非常期待接下来的研究。