【转载请注明出处】chenrudan.github.io
本文是David Silver强化学习公开课第六课的总结笔记。这一课主要讲了由于现实问题中状态数过多导致无法直接求解出值函数,从而通过梯度下降的方式来求解真实值函数的近似函数形式。
本课视频地址:RL Course by David Silver - Lecture 6: Value Function Approximation
本课ppt地址:http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching_files/FA.pdf
文章的内容是课程的一个总结和讨论,会按照自己的理解来组织。个人知识不足再加上英语听力不是那么好可能会有一些理解不准的地方,欢迎一起讨论。
建了一个强化学习讨论qq群,有兴趣的可以加一下群号595176373或者扫描下面的二维码。

1.内容回顾
前面的课大致上讲解了解决各种情况下的MDP问题,目的就是为了从某个状态开始选择最好的执行方法一直运行到终止状态,要么是求在某个状态$S$下的value function,要么是求在某个状态下$S$执行某个动作$A$的action-value function,但现实中有不少问题的状态$S$的取值和动作$A$非常多,例如围棋的361个点位,每个点位会出现黑白空三种情况,那么就有$3^{361} \approx 10^{170}$种状态,如果算出每种状态下的真实value function既没有足够的内存也没有足够的计算能力,此外比较接近的状态它们的值函数取值应该是很相似的,这是一种泛化能力。
也就是说需要算法来求解近似的$V(S)$和$Q(S,A)$,并且针对未知的状态有比较强的泛化能力。这种近似算法称之为function approximation,用$\hat{v}(s,w)$来近似真实值函数,用$\hat{q}(s,a,w)$来近似真实动作值函数,其中$w$是近似函数的更新参数,例如神经网络的权重。近似的方法有特征线性组合、神经网络、决策树、最近邻等等。以神经网络为例,输入是状态$S$,那么输出就是$\hat{v}(s,w)$,即把近似值函数用神经网络实现出来。
2.随机梯度下降
假设近似值函数对$w$是可微的,最简单的就是用梯度下降,假设输入状态用特征向量$x(S) = (x_1(S), x_2(S), …, x_n(S))^T$,例如机器人的行走状态,第一个特征是距离横向基准位置多远,第二个特征是距离纵向基准位置多远等等。目标函数是$J(w) = E_{\pi}[(v_{\pi}(S) - \hat{v}(S,w))^2]$。从而随机梯度下降求得权重改变量为$\Delta w = \alpha(v_{\pi}(S) - \hat{v}(S,w)) \bigtriangledown_w \hat{v}(S,w) = \alpha(v_{\pi}(S) - \hat{v}(S,w))x(S)$。
但是在强化学习中,$v_{\pi}(S)$是未知的,无法用来当做监督信息,因此要用别的东西来代替,从而可以根据Monte-Carlo Learning和Temporal Difference Learning两种方法来考虑。
Monte-Carlo Learning中针对某个状态叠加每个episode中在这个状态上产生的return,因为每个episode是走到了终止状态的,所以可以向初始状态的方向将return传播回来。而实际上值函数就是return的期望,所以基于MC方法就是用$G_t$代替$v_{\pi}(S)$
Temporal Difference Learning中针对某个状态估计下一个时刻可能获得的return,由immdiate reward和上一次更新的值函数构成,也称为TD target,从而更新当前时刻的值函数,因此用$R_{t+1} + \gamma \hat{v}(S_{t+1},w)$来替换$v_{\pi}(S)$。替换后发现括号内的这一项就是TD error。同样的TD($\lambda$)也是替换成第四课的公式即可。
而动作值函数也是差不多的,就是替换,这里就不提了,参考[1]。
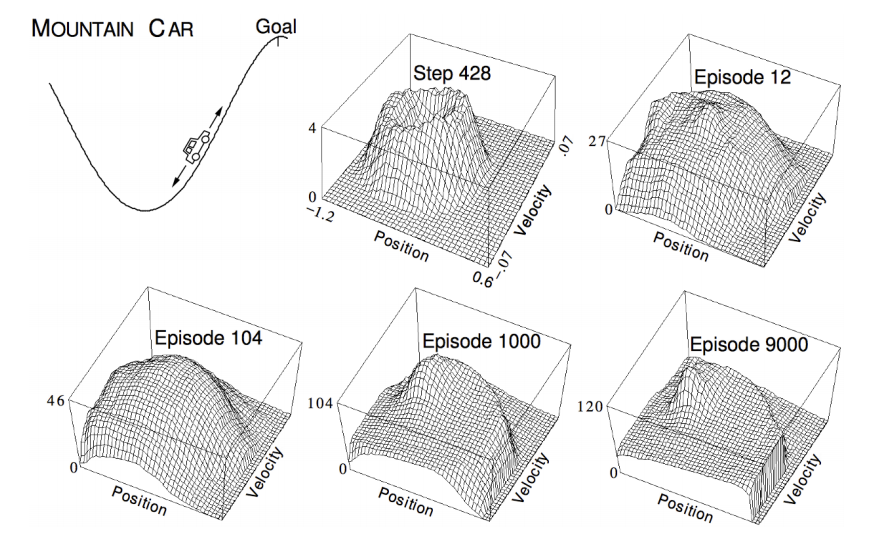
在强化学习中,有个比较经典的例子就是汽车爬山[2],车会在凹的山谷中来回启动,不同的高度上汽车需要学会利用势能来到达对面的山顶,这个问题中的状态就是汽车所处的位置和当前的速度(个人觉得当前的速度应该是action,在不同的位置人控制不同的速度,但是David课中说action是选择加速还是不加速),曲面的起伏代表了value function。通过图中多执行多个episode得到了值函数的表达形式。
3. DQN
此处讲batch methods说”梯度下降的方法针对一个sample,只利用一次,更新一次梯度之后就不再使用了,并没有挖掘出这个sample所有信息,因此需要用batch methods来重复的利用sample并找到最佳拟合值函数,拟合所有看到过的sample” ,这个意思我觉得并不重要,如果用神经网络来学习参数必然会多次迭代sample,所以直接介绍DQN。
Deep Q-Networks,是DeepMind团队提出的一种深度强化学习方法,具体算法如下:
- 根据$\epsilon-$greedy policy选择一个动作$a_t$(这里没具体说policy是哪个,根据Q-Learning,这里应该是behaviour policy)。
- 选择完$a_t$后会产生下个时刻的状态和奖赏,将多个转移序列$(s_t, a_t, r_{t+1}, s_{t+1})$保存在称为reply memory的集合D中
- 从D中随机选择一些转移序列$(s,a,r,s’)$,基于这些和固定参数$w^-$计算Q-Learning的target即$r + \gamma \underset{a’}{max}Q(s’,a’;w^-)$
- 通过随机梯度下降方法来优化Q-Leanring的target和近似函数$Q(s,a;w)$的均方差。其中近似函数也称为Q-network。
最后十分钟讲了一下如何结合最小二乘法与MC/TD,令导数等于0再推导,流程跟梯度下降一样,这里就不提了,经过这几课大致可以看出强化学习要求解的核心就是policy和值函数,这一课可以看出值函数的具体形式可以用神经网络表示出来,即把状态变换成一个特征向量当做输入,经过神经网络得到值函数输出。
[1] http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching_files/FA.pdf