【机器学习算法系列之二】浅析Logistic Regression

【转载请注明出处】chenrudan.github.io

本文是受rickjin老师的启发，谈谈关于logistic regression的一些内容，虽然已经有珠玉在前，但还是做一下自己的总结。在查找资料的过程中，越看越觉得lr实在是博大精深，囊括的内容太多太多了，本文只能浅显的提到某些方面。文章的内容如下:

1. 起源
2. 模型介绍与公式推导
- 2.1 Logistic Distribution
- 2.2 Binomial logistic regression model
3. 解法
4. 正则化
- 4.1 过拟合
- 4.2 正则化的两种方法
5. 逻辑回归与其他模型关系
6. 并行化
7. 小结
8. 引用

1. 起源

logistic regression的起源主要分为几个阶段，从开始想到logistic这个词，到发现logistic function，再推导出logit function，最后才命名logistic regression。这些过程都是大量的研究者们共同努力发现的，只是在历史的长河中，很多人被渐渐遗忘了。

logistic起源于对人口数量增长情况的研究，最重要的工作是Pierre François Verhulst在1838年提出了对人口增长的公式描述(这人是个比利时人，写的文章是法语的，一个字都看不懂，下面的内容都是看了一篇将研究人口数量增长发展历程的书[1]才知道的…)，他博士毕业于根特大学的数学系，是个数学教授和人口学家。在1835年Verhulst的同乡人Adolphe Quetelet发表了一篇关于讨论人口增长的文章，文中认为人口不可能一直是几何(指数)增长，而会被与增长速度平方成比例的一种阻力而影响，但是这篇论文只有猜想没有数学理论基础，却极大的启发了Verhulst。因此在1838年Verhulst发表了关于人口数量增长的论文，就是在这篇论文里面他推导出了logistic equation，文章中谈到一个重要观点，随着时间的增加，一个国家的大小（我理解为资源）和这个国家人们的生育能力限制了人口的增长，人口数量会渐渐趋近一个稳定值。厉害的是他将这个过程用公式给描述出来了，他从人口数量增长的速度公式入手，即人口数量$P(t)$对时间t的导数:

$$
\frac{\partial P}{\partial t} = rP(1-\frac{P}{K})
$$

其中$K$就是他认为人口数量稳定的值，当$P(t)$远小于$K$时，求导公式后一项约等于0，那么就变成了$\frac{\partial P}{\partial t} \simeq rP$，这个阶段人口增长速度与人口数量和一个常数的乘积成正比，并且在渐渐变大。然后对这个式子求解一阶线性微分方程得到$P(t)\simeq P(0)e^{rt}$。当$P(t)$接近$K$时，人口增长速度开始渐渐变小，同样求解二阶微分方程(论文中是将二阶转化成一阶求解)，然后将二者整合在一起得到最初的形式。

$$
P(t) = \frac{P(0)e^{rt}}{1+P(0)(e^{rt}-1)/K}
$$

他将法国英国等过十几年的人口实际数据拿来跟这个公式对比之后发现确实拟合的很不错。但他当时并没有那么多年的数据，下图1是在他过世以后人们总结的300年来的人口增长分布，可以看到非常漂亮的拟合了logisitc分布的累积分布函数走势。但是当时这个公式并没有名字，直到1845年他发表了另外一篇重要文章[2]，他给这个公式起了一个名字——“logistic”，此外在这篇文章中，他发现在$P(t)<K/2$的时候，$P(t)$呈凸增长趋势，在$P(t)>K/2$时$P(t)$呈凹增长(通过求二阶导来分析，这里略)。这个增长的趋势类似logistic分布的概率密度函数。

图1 比利时的人口增长数量图(图来源[2])

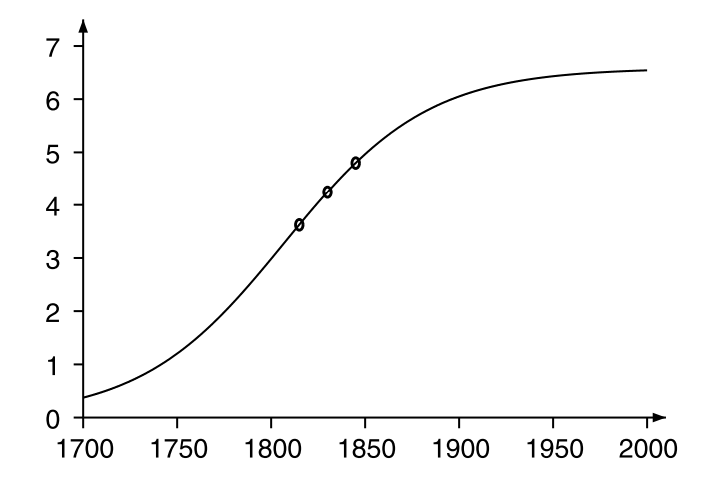
然而在后来的几十年内人们都没有意识到这个工作的重要性，很多人都独立的研究出了这个增长现象，直到1922年一个叫做Raymond Pearl的人口学家注意到Verhulst在1838年就已经提出了这个现象和公式，并在他的文章中也使用了logistic function来称呼它，并且沿用至今。在1920年Pearl[3]在研究美国人口增长规律时提出了另外一种表示logistic function的方法。

$$
y = \frac{be^{ax}}{1+ce^{ax}}
$$

基于这个表达式，Joseph Berkson在1944年提出了logit function，$logit = In(\frac{1-Q}{Q})$，假如$Q = \frac{1}{1+e^{a-bx}}$，结果就是$logit=a-bx$。

后来，在1958年David Cox提出了logistic regression[4]。他的文章是为了解决这样一个问题，有一组取值为0，1的观测值，它们的取值$Y_i$依赖于一些独立变量$x_i$，当$Y_i=1$时对应的概率为$\theta_i=pr(Y_i = 1)$。由于$\theta_i$限制在[0,1]之间，因此假设$\theta_i$与$x_i$的关系符合logit function，即$logit\theta_i \equiv log{\frac{\theta_i}{1-\theta_i}} = \alpha + \beta x_i$，文章主要在分析如何求解里面的参数$\beta$，这里就不提了。由于用到了logistic function，而这个问题本身又个回归问题(建立观测值与独立变量之间的关系)，因而它被称呼为logistic regression。

貌似Cox在这篇文章中并不是刻意提出logistic regression，但确实这个词第一次出现就是在这篇文章中，虽然Cox之前已经有很多人做过这方面的研究了，但是他们没给个名字，因此Cox成了提出logistic regression的人。这个故事告诉我们一个道理，无论是发文章还是写软件一定要取一个言简意赅又好听又好记的名字…

以上是逻辑回归的历史发展中比较有代表性的几件事(我认为的…还有好多论文没时间细看…)，J.S Cramer[5]在他的文章中有更加详细的讨论。它是由数学家对人口发展规律研究得出，后来又被应用到了微生物生长情况的研究，后来又被应用解决经济学相关问题，直到发展到今天作为一个非常重要的算法而存在于各行各业。逻辑回归作为Regression Analysis的一个分支，它实际上还受到很多Regression Analysis相关技术的启发，例如Berkson就是基于probit function提出的logit function。光它的起源到应用就能写一本书出来了，难怪rickjin老师说lr其实非常非常复杂…

2.模型介绍与公式推导

上面说过了逻辑斯蒂回归的起源，下面讨论一下完整的模型，首先介绍一下何为逻辑斯蒂分布，再由逻辑斯蒂分布推出逻辑回归。

2.1 Logistic Distribution

随机变量X服从逻辑斯蒂分布，即X的累积分布函数为上文提到过的logistic function。对分布函数求导得到了概率密度函数。公式如下，参数影响参考图2(图来自维基百科，它的参数s就是统计学习方法上的$\gamma$)

$$
F(x) = P(X \leqslant x) = \frac{1}{1+e^{-(x-\mu)/\gamma}}
$$

$$
f(x) = F’(x) = \frac{e^{-(x-\mu)/\gamma}} { \gamma (1+e^{-(x-\mu)/\gamma})^2 }
$$

图2 不同参数对logistic分布的影响(图片来源维基百科)

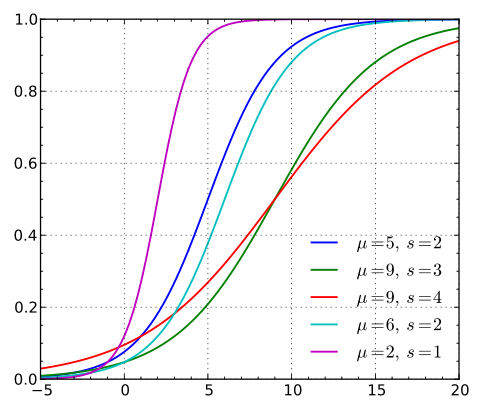
可以看到$\mu$影响的是中心对称点的位置，$\gamma$越小中心点附近增长的速度越快。而常常在深度学习中用到的非线性变换sigmoid函数是逻辑斯蒂分布的$\gamma=1,\mu=0$的特殊形式。

2.2 Binomial logistic regression model

图3 数据示例

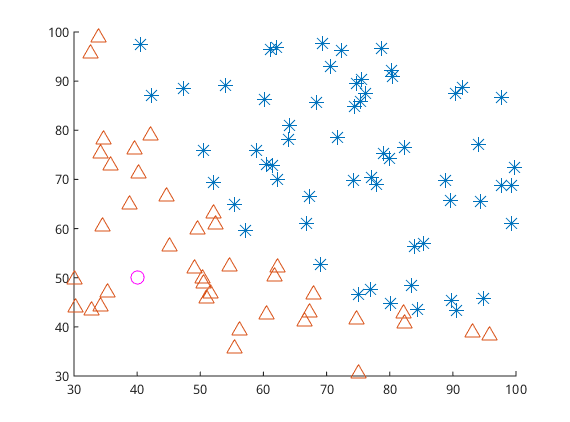
逻辑回归是为了解决分类问题，根据一些已知的训练集训练好模型，再对新的数据进行预测属于哪个类。如图3所示，有一些属于两个类的数据，目标是判断圆圈属于哪一类。也就是说逻辑回归的目标是找到一个有足够好区分度的决策边界，从而能够将两类很好的分开。假设已经存在这样一个边界，针对于图中这种线性可分的情况，这条边界是
输入特征向量的线性组合，假设输入的特征向量为$x\in R^n$(图中输入向量为二维)，$Y$取值为0，1。那么决策边界可以表示为$w_1x_1+w_2x_2+b=0$，假如存在一个例子使得$h_w(x) = w_1x_1+w_2x_2+b > 0$，那么可以判断它类别为1，这个过程实际上是感知机，即只通过决策函数的符号来判断属于哪一类。而逻辑回归需要再进一步，它要找到分类概率$P(Y=1)$与输入向量$x$的直接关系，然后通过比较概率值来判断类别，而刚好上文中的logit function能满足这样的要求，它令决策函数的输出值$w^Tx+b$等于概率值比值取对数$log{\frac{P(Y=1|x)}{1-P(Y=1|x)}}$，求解这个式子得到了输入向量$x$下导致产生两类的概率为:

$$
P(Y=1|x)=\frac{e^{w\cdot x+b}}{1+e^{w\cdot x+b}} :::::::::(1)
$$

$$
P(Y=0|x)=\frac{1}{1+e^{w\cdot x+b}} :::::::::(2)
$$

其中$w$称为权重，$b$称为偏置，其中的$w\cdot x+b$看成对$x$的线性函数。然后对比上面两个概率值，概率值大的就是x对应的类。有时候为了书写方便，会将$b$写入$w$，即$w=(w_0, w_1, …, w_n)$其中$w_0=b$，并取$x_0 = 1$。又已知一个事件发生的几率odds是指该事件发生与不发生的概率比值，二分类情况下即$\frac {P(Y=1|x)}{P(Y=0|x)} = \frac {P(Y=1|x)}{1-P(Y=1|x)}$。取odds的对数就是上面提到的logit function，$logit(P(Y=1|x)) = log\frac {P(Y=1|x)}{1-P(Y=1|x)} = w\cdot x$。从而可以得到一种对逻辑回归的定义，输出$Y=1$的对数几率是由输入$x$的线性函数表示的模型，即逻辑斯蒂回归模型(李航.《统计机器学习》)。而直接考察公式1可以得到另一种对逻辑回归的定义，线性函数的值越接近正无穷，概率值就越接近1；线性值越接近负无穷，概率值越接近0，这样的模型是逻辑斯蒂回归模型(李航.《统计机器学习》)。因此逻辑回归的思路是，先拟合决策边界(这里的决策边界不局限于线性，还可以是多项式)，再建立这个边界与分类的概率联系，从而得到了二分类情况下的概率。这里有个非常棒的博文[6]推荐，阐述了逻辑回归的思路。

在推导多分类的问题时，是假设$w_1^Tx + b_1 = \frac{P(Y=1|x)}{P(Y=K|x)}$、$w_2^Tx + b_2 = \frac{P(Y=2|x)}{P(Y=K|x)}$…等，再推导出$P(Y=K|x) = \frac{1}{1+\sum_{k=1}^{K-1}e^{w_k^Tx}}$、$P(Y=1|x) = \frac{e^{w_1^Tx}}{1+\sum_{k=1}^{K-1}e^{w_k^Tx}}$等。

有了上面的分类概率，就可以建立似然函数，通过极大似然估计法来确定模型的参数。设$P(Y=1|x)=h_w (x)$，似然函数为$\prod [h_w(x_i)]^{y_i}[1-h_w(x_i)]^{(1-y_i)}$，对数似然函数为

$$
L(w) = \sum {i=1}^{N}logP(y_i|x_i;w) = \sum\{i=1}^{N}[y_ilog h_w (x_i) +(1-y_i)log(1-h_w(x_i))] :::::::::(3)
$$

3.解法

优化逻辑回归的方法有非常多[7]，有python的不同实现[8]，这里只谈谈梯度下降，牛顿法和BFGS。优化的主要目标是找到一个方向，参数朝这个方向移动之后使得似然函数的值能够减小，这个方向往往由一阶偏导或者二阶偏导各种组合求得。逻辑回归的损失函数是

$$
min J(w) = min {-\frac{1}{m}[\sum_{i=1}^{m}y_ilog h_w (x_i) + (1-y_i)log(1-h_w(x_i))]} :::::::::(4)
$$

先把$J(w)$对$w_j$的一阶二阶偏导求出来，且分别用$g$和$H$表示。$g$是梯度向量，$H$是海森矩阵。这里只考虑一个实例$y_i$产生的似然函数对一个参数$w_j$的偏导。

$$
g_j = \frac{\partial J(w)} {\partial w_j} = \frac{y^{(i)}}{h_w(x^{(i)})}h_w(x^{(i)})(1-h_w(x^{(i)}))(-x_{j}^{(i)})+(1-y^{(i)})\frac {1}{1-h_w(x^{(i)})}h_w(x^{(i)})(1-h_w(x^{(i)}))x_j^{(i)}=(y^{(i)}-h_w(x^{(i)}))x^{(i)} :::::::::(5)
$$

$$
H_{mn} = \frac {\partial^2 J(w)} {\partial w_m \partial w_n} =h_w(x^{(i)})(1-h_w(x^{(i)}))x^{(i)}_mx^{(i)}_n :::::::::(6)
$$

这几种方法一般都是采用迭代的方式来逐步逼近极小值，需要给定参数$w_0$作为起点，并且需要一个阈值$\epsilon$来判断迭代何时停止。

3.1 梯度下降法

梯度下降是通过$J(w)$对$w$的一阶导数来找下降方向，并且以迭代的方式来更新参数，更新方式为$w_j^{k+1} = w_j^k + \alpha g_j$，$k$为迭代次数。每次更新参数后，可以通过比较$||J(w^{k+1})-J(w^k)||$或者$||w^{k+1}-w^k||$与某个阈值$\epsilon $大小的方式来停止迭代，即比阈值小就停止。

3.2 牛顿法

牛顿法的基本思路是，在现有极小点估计值的附近对f(x)做二阶泰勒展开，进而找到极小点的下一个估计值[9]。假设$w^k$为当前的极小值估计值，那么有

$$
\varphi (w) = J(w^k) + J’(w^k)(w-w^k)+\frac{1}{2}J’’(w^k)(w-w^k)^2 :::::::::(7)
$$

然后令$\varphi’(w)=0$，得到了$w=w^k-\frac{J’(w^k)}{J’’(w^k)}$。因此有迭代更新式，

$$
w^{k+1} = w^k - \frac{J’(w^k)}{J’’(w^k)} = w^k - H_k^{-1}\cdot g_k :::::::::(8)
$$

此方法中也需要一个阈值$\epsilon$，当$||g_k|| < epsilon$时停止迭代。此外，这个方法需要目标函数是二阶连续可微的，本文中的$J(w)$是符合要求的。

3.3 BFGS

由于牛顿法中需要求解二阶偏导，这个计算量会比较大，而且有时目标函数求出的海森矩阵无法保持正定，因此提出了拟牛顿法。拟牛顿法是一些算法的总称，它们的目标是通过某种方式来近似表示森海矩阵(或者它的逆矩阵)。例如BFGS就是一种拟牛顿法，它是由四个发明人的首字母组合命名，是求解无约束非线性优化问题最常用的方法之一。目标是用迭代的方式逼近海森矩阵$H$，假设这个逼近值为$B^k\approx H^k$，那么希望通过计算$B^{k+1} = B^k + \Delta B^k$能够达到目的。并且假设$\Delta B^k = \alpha uu^T + \beta vv^T$，而由3.2可知，$\Delta w = w^{k+1}-w^k = (H^{-1})^{k+1}(g^{k+1}-g^k) = (H^{-1})^k\Delta g$，将$B^{k+1}$的更新式代入，可以得到

$$
\Delta g = B^k\Delta g + (\alpha u^T\Delta w)u + (\beta v^T\Delta w)v :::::::::(9)
$$

此处，直接令$\alpha u^T\Delta w=1$、$\beta v^T\Delta w=-1$、$u=\Delta g$和$v=B^k\Delta w$，那么可以求得$\alpha = \frac {1}{(\Delta g)^T\Delta w}$和$\beta = -\frac{1}{(\Delta w)^TB^k\Delta w}$。从而再代入求$\Delta B^k$的式子就可以得到更新的式子

$$
\Delta B^k = \frac {\Delta g(\Delta g)^T}{(\Delta g)^T\Delta w} - \frac {B^k\Delta w(\Delta w)^TB^k}{(\Delta w)^TB^k\Delta w} :::::::::(10)
$$

这里还会对(10)进行变换，通过Sherman-Morrison公式直接求出$(B^{-1})^{k+1}$与$(B^{-1})^k$，用$D^{k+1}$和$D^k$来表。更新公式变成了

$$D^{k+1} = (I-\frac {\Delta w (\Delta g)^T}{(\Delta g)^T\Delta w}) D^k (I - \frac {\Delta g (\Delta w)^T}{(\Delta g)^T\Delta w}) + \frac {\Delta w (\Delta w)^T}{(\Delta g)^T\Delta w} :::::::::(11)$$

用BFGS来更新参数的流程如下:

确定改变量，$(\Delta w)^k= -D^k\cdot g^k$
更新参数，$w^{k+1} = w^k + \lambda (\Delta w)^k$
求出$\Delta g = g^{k+1} -g^k$
由(11)求出$D^{k+1}$

式子的系数$\lambda=argmin J(w^k + \lambda (\Delta w)^k)$，即在求得下降方向上来从很多值中搜索最优的下降大小，这里我觉得可以用学习率替代。因此，这个更新方法跟牛顿法的区别是，它是在更新参数$w$之后更新一下近似森海矩阵的值，而牛顿法是在更新$w$之前完全的计算一遍森海矩阵。还有一种从计算上改进BFGS的方法称为L-BFGS，不直接存储森海矩阵，而是通过存储计算过程中产生的部分$\Delta w(g)_{k-m+1,k-m+2,…,k}$，从而减少了参数存储所需空间。

4.正则化

正则化不是只有逻辑回归存在，它是一个通用的算法和思想，所以会产生过拟合现象的算法都可以使用正则化来避免过拟合，在谈正则化之前先聊聊什么是过拟合。

4.1 过拟合

之前的模型介绍和算法求解可以通过训练数据集(图2中的三角形和星形)将分类模型训练好，从而可以预测一个新数据(例如图2中的粉色圆圈)的分类，这种对新数据进行预测的能力称为泛化能力。而对新数据预测的结果不好就是泛化能力差，一般来说泛化能力差都是由于发生了过拟合现象。过拟合现象是指对训练数据预测很好但是对未知数据预测不行的现象，通常都是因为模型过于复杂，或者训练数据太少。即当$\frac{complexity\: of \:the \:model}{training \:set \:size}$比值太大的情况下会发生过拟合。模型复杂体现在两个方面，一是参数过多，二是参数值过大。参数值过大会导致导数非常大，那么拟合的函数波动就会非常大，即下图所示，从左到右分别是欠拟合、拟合和过拟合。

图4 同样数据下欠拟合，拟合和过拟合(图片来源[12])

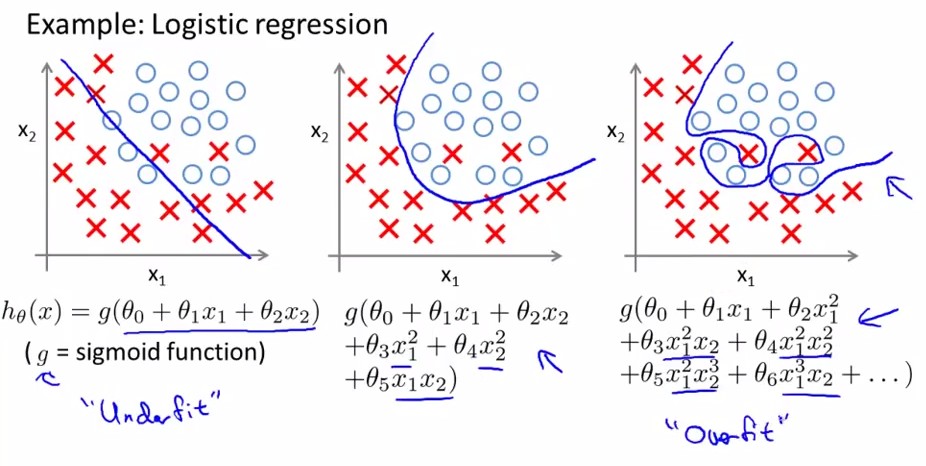
在模型过于复杂的情况下，模型会学习到很多特征，从而导致可能把所有训练样本都拟合到，就像上图中一样，拟合的曲线将每一个点都正确的分类了。举个例子，假如要预测一个房子是贵还是便宜，房子的面积和所属的地区是有用的特征，但假如训练集中刚好所有贵的房子都是开发商A开发，便宜的都是开发商B开发，那么当模型变复杂能学习到的特征变多之后，房子是哪个开发商的会被模型认为是个有用特征，但是实际上这点不能成为判断的标准，这个现象就是过拟合。因此在这个例子中可以看到，解决的方法有两个，一个是减少学习的特征不让模型学到开发商的特征，一是增加训练集，让训练集有贵房子是B开发的样本。

从而，解决过拟合可以从两个方面入手，一是减少模型复杂度，一是增加训练集个数。而正则化就是减少模型复杂度的一个方法。

4.2 正则化的两种方法

由于模型的参数个数一般是由人为指定和调节的，所以正则化常常是用来限制模型参数值不要过大，也被称为惩罚项。一般是在目标函数(经验风险)中加上一个正则化项$\Phi(w)$即

$$
J(w) = -\frac{1}{m}[\sum_{i=1}^{m}y_ilog h_w (x_i) + (1-y_i)log(1-h_w(x_i))] + \lambda \Phi(w) :::::::::(12)
$$

而这个正则化项一般会采用L1范数或者L2范数。其形式分别为$\Phi (w)=||x||_1$和$\Phi (w)=||x||_2 $。

首先针对L1范数$\phi (w) = |w|$，当采用梯度下降方式来优化目标函数时，对目标函数进行求导，正则化项导致的梯度变化当$w_j>0$是取1，当$w_j<0$时取-1.

从而导致的参数$w_j$减去了学习率与(13)式的乘积，因此当$w_j$大于0的时候，$w_j$会减去一个正数，导致$w_j$减小，而当$w_j$小于0的时候，$w_j$会减去一个负数，导致$w_j$又变大，因此这个正则项会导致参数$w_j$取值趋近于0，也就是为什么L1正则能够使权重稀疏，这样参数值就受到控制会趋近于0。L1正则还被称为 Lasso regularization。

然后针对L2范数$\phi(w) = \sum_{j=1}^{n}w_j^2$，同样对它求导，得到梯度变化为$\frac{\partial \Phi(w)}{\partial w_j} = 2w_j$(一般会用$\frac{\lambda}{2}$来把这个系数2给消掉)。同样的更新之后使得$w_j$的值不会变得特别大。在机器学习中也将L2正则称为weight decay，在回归问题中，关于L2正则的回归还被称为Ridge Regression岭回归。weight decay还有一个好处，它使得目标函数变为凸函数，梯度下降法和L-BFGS都能收敛到全局最优解。

需要注意的是，L1正则化会导致参数值变为0，但是L2却只会使得参数值减小，这是因为L1的导数是固定的，参数值每次的改变量是固定的，而L2会由于自己变小改变量也变小。而(12)式中的$\lambda$也有着很重要的作用，它在权衡拟合能力和泛化能力对整个模型的影响，$\lambda$越大，对参数值惩罚越大，泛化能力越好。

此外，从贝叶斯的角度而言，正则化项实际上是给了模型一个先验知识，L2正则相当于添加了一个均值为0协方差为$1/\lambda$的高斯分布先验(将L2正则表示为$\frac{\lambda}{2}w^Tw$)，当$\lambda$为0，即不添加正则项，那么可以看成协方差是无穷大，$w$可以不受控制变成任意大。当$\lambda$越大，即协方差越小，那么参数值的取值方差会变小，模型会趋向于稳定(参考[10]最高票答案)。

5. 逻辑回归与其他模型的关系

5.1 逻辑回归与线性回归

在谈两者关系之前，需要讨论的是，逻辑回归中使用到的sigmoid函数到底起到了什么作用。下图的例子中，需要判断肿瘤是恶性还是良性，其中横轴是肿瘤大小，纵轴是线性函数$h_w(x)=w^Tx+b$的取值，因此在左图中可以根据训练集(图中的红叉)找到一条决策边界，并且以0.5作为阈值，将$h_w(x) \geqslant 0.5$情况预测为恶性肿瘤，这种方式在这种数据比较集中的情况下好用，但是一旦出现如右图中的离群点，它会导致学习到的线性函数偏离(它产生的权重改变量会比较大)，从而原先设定的0.5阈值就不好用了，此时要么调整阈值要么调整线性函数。如果我们调节阈值，在这个图里线性函数取值看起来是0～1，但是在其他情况下可能就是从$-\infty$到$\infty$，所以阈值的大小很难确定，假如能够把$w^Tx+b$的值变换到一个能控制的范围那么阈值就好确定了，所以找到了sigmoid函数，将$w^Tx+b$值映射到了(0,1)，并且解释成概率。而如果调节线性函数，那么最需要的是减少离群点的影响，离群点往往会导致比较大的$|w^Tx+b|$值，通过sigmoid函数刚好能够削弱这种类型值的影响，这种值经过sigmoid之后接近0或者1，从而对$w_j$的偏导数为$h_w(x^{(i)})(1-h_w(x^{(i)}))x_j^{(i)}$，无论接近0还是1这个导数都是非常小的。因此可以说sigmoid在逻辑回归中起到了两个作用，一是将线性函数的结果映射到了(0,1)，一是减少了离群点的影响。

图5 良性恶性肿瘤分类(图来源[12])

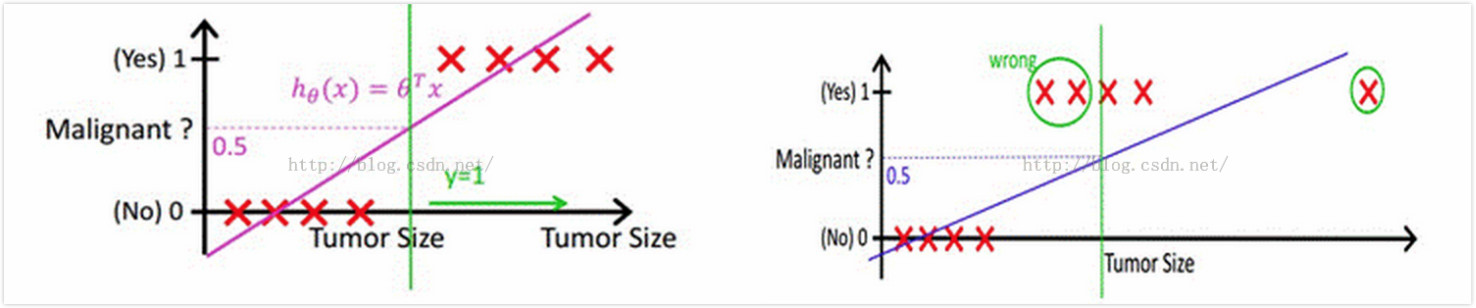
有了上面的分析基础，再来看看逻辑回归和线性回归的关系(线性回归我这里就不展开说了，不清楚的可以看看[11])，有的人觉得逻辑回归本质上就是线性回归，它们俩都要学习一个线性函数，逻辑回归无非是多加了一层函数映射，但是我对线性回归的理解是在拟合输入向量x的分布，而逻辑回归中的线性函数是在拟合决策边界，它们的目标是不一样的。所以我不觉得逻辑回归比线性回归好，它们俩要解决的问题不一样。但它们都可以用一个东西来概括，那就是广义线性模型GLM(Generalized linear models)[12]。先介绍何为指数簇(exponential family)，当某个随机变量的概率分布可以表示为$p(y;\eta )=b(y)exp(\eta^TT(y)-a(\eta))$时就可以说它属于指数簇，通过调整$\eta$可以获得不同的分布。对应于线性回归与逻辑回归的高斯分布与伯努利分布就是属于指数簇的，例如取$T(y)=y$、$a(\eta)=-log(1-\phi) = log(1+e^\eta)$以及$b(y)=1$代入上式得到$p(y;\eta) =exp(ylog(\frac{\phi}{1-\phi}) + log(1-\phi)) =exp(ylog{\phi}+log(1-\phi)) = \phi^{y}(1-\phi)^{1-y}$。

GLM需要满足下面三个条件。

在给定观测值x和参数w情况下，输出y服从参数为$\eta$的指数簇分布
预测的值$h_w(x) = E[y|x]$
$\eta = w^Tx$

因此，选择合适的参数就能分析出线性回归和逻辑回归都是GLM的一种特例，有时会看到有的人会从GLM出发将逻辑回归的公式给推导出来。总之，线性回归和逻辑回归是属于同一种模型，但是它们要解决的问题不一样，前者解决的是regression问题，后者解决的是classification问题，前者的输出是连续值，后者的输出是离散值，而且前者的损失函数是输出y的高斯分布，后者损失函数是输出的伯努利分布。

5.2 逻辑回归与最大熵

最大熵在解决二分类问题时就是逻辑回归，在解决多分类问题时就是多项逻辑回归。为了证明最大熵模型跟逻辑回归的关系，那么就要证明两者求出来的模型是一样的，即求出来的h(x)的形式应该是一致的。由于最大熵是通过将有约束条件的条件极值问题转变成拉格朗日对偶问题来求解，模型的熵为

$$-\sum_{v=1}^k\sum_{i=1}^m h(x^{(i)})_v log(h(x^{(i)})_v) :::::::::(14)$$

并假设约束条件如下，其中$v,u$是输出类别的index，$j$是对应输入向量$x$的index，$A(u,y^{(i)})$是指示函数，两个值相等输出1，其他输出0[13]。而第三个约束是通过令公式(5)等于0得来的，它的意义是参数$w_{u,j}$最好的取值是让每一个样本i对应$h(x^{(i)})_u$的行为接近指示函数$A(u,y^{(i)})$。

$$
\begin{cases}
h(x)_v\geqslant 0 & \text{ always } \\
\sum_{v=1}^k h(x)_v = 1 & \text{ always } \\
\sum_{i=1}^m h(x^{(i)})u x^{(i)}_j = \sum\{i=1}^m A(u,y^{(i)})x^{(i)}_j & \text{ for all } : u, j
\end{cases} :::::::::(15)
$$

通过约束条件(15)可以直接推导出softmax的公式。基于这一点，再回过头来看《统计学习方法》上的约束条件，如果假设$P(y|x) = h(x)$，公式左边的$f(x,y)$实际上取值一直为1，那么这两个约束条件实际上是一样的。

$$\sum_{x,y} \widetilde{P(x)}P(y|x)f(x,y) = \sum_{x,y} \widetilde{P(x,y)}f(x,y) :::::::::(16) $$

因此，可以这样说，最大熵在解决二分类问题时就是逻辑回归，在解决多分类问题时就是多项逻辑回归。此外，最大熵与逻辑回归都称为对数线性模型(log linear model)。

5.3 逻辑回归与svm

逻辑回归和svm作为经典的分类算法，被放在一起讨论的次数特别多，知乎和Quora上每种意见都非常有意思都从不同角度有分析，建议都可以看看[14][15][16]。这里只讨论一些我赞同的观点。要是不清楚svm的由来，建议看JerryLead的系列博客[17]，我这里就不提了。

相同点:

都是分类算法
都是监督学习算法
都是判别模型
都能通过核函数方法针对非线性情况分类
目标都是找一个分类超平面
都能减少离群点的影响

不同点:

损失函数不同，逻辑回归是cross entropy loss，svm是hinge loss
逻辑回归在优化参数时所有样本点都参与了贡献，svm则只取离分离超平面最近的支持向量样本。这也是为什么逻辑回归不用核函数，它需要计算的样本太多。并且由于逻辑回归受所有样本的影响，当样本不均衡时需要平衡一下每一类的样本个数。
逻辑回归对概率建模，svm对分类超平面建模
逻辑回归是处理经验风险最小化，svm是结构风险最小化。这点体现在svm自带L2正则化项，逻辑回归并没有
逻辑回归通过非线性变换减弱分离平面较远的点的影响，svm则只取支持向量从而消去较远点的影响
逻辑回归是统计方法，svm是几何方法

5.4 逻辑回归与朴素贝叶斯

这两个算法有一些相似之处，并且在对比判别模型和生成模型，它们作为典型的分类算法经常被提及，因此这里也做一个小小的总结。

相同点是，它们都能解决分类问题和都是监督学习算法。此外，有意思的是，当假设朴素贝叶斯的条件概率$P(X|Y=c_k)$服从高斯分布时Gaussian Naive Bayes，它计算出来的$P(Y=1|X)$形式跟逻辑回归是一样的[18]。

不同的地方在于，逻辑回归为判别模型求的是$p(y|x)$，朴素贝叶斯为生成模型求的是$p(x,y)$。前者需要迭代优化，后者不需要。在数据量少的情况下后者比前者好，数据量足够的情况下前者比后者好。由于朴素贝叶斯假设了条件概率$P(X|Y=c_k)$是条件独立的，也就是每个特征权重是独立的，如果数据不符合这个情况，朴素贝叶斯的分类表现就没有逻辑回归好。

5.5 逻辑回归与能量模型

(3月3日补充)

基于能量的模型不是一个具体的算法，而是一种框架思想，它认为输入输出变量之间的依赖关系用一个值表示$E(x,y)$，这个值称为能量，对关系建模的这个函数叫能量函数。如果在保持输入变量不变的情况下，对应正确输出时能量低，对应错误输出时能量高，那么这个模型就是有用的。

因此当给定了训练集S，能量模型的构造和训练由四部分组成[19]:

有合适的能量函数$E(W,Y,X)$
inference算法，针对一个给定的输入变量X和能量函数形式，找到一个Y值使得能量最小，即$Y^* = argmin_{Y\in y}E(W,Y,X) $
有loss函数$L(W,S)$，用来衡量在训练集S下能量函数的好坏
learning算法，用来找合适的参数W，在一系列能量函数中选择让损失函数最小化的能量函数。

可以看出13步通过选择不同的能量函数和损失函数来构造不同的模型，24步是如何训练这样的一个模型。

因此当我们假设要解决二分类问题时，y取值为-1和1，如果假设能量函数为$E(W,Y,X)=-YG_w(X)=W^TX$，损失函数采用negative log-likelihood loss，那么可以求得损失函数具体形式为$L_{nll}(W,S)=\frac{1}{P}\sum_{i=1}^{P}log(1+exp(-2Y^iW^TX))$，这个形式与把(1)(2)代入公式(3)后得到的损失函数公式是一致的，说明这种组合下，产生的算法就是逻辑回归。因此逻辑回归是能量模型的一种特例。

而此处，同样针对二分类问题，假如能量函数保持不变，损失函数采用hinge loss，并加上一个正则化项，那么就能够推导出SVM的损失函数表达式(SVM的核函数体现在能量函数中，这里为了方便解释没有具体展开说)。这也是为什么说逻辑回归与svm最本质的区别就是损失函数不同。

6. 并行化

由于找不到特别多的并行化资料，这里就分析一下博主冯扬给出的实现[20]。实际上逻辑回归的并行化最主要的目标就是计算梯度。将目标的label变为-1和1，那么梯度公式可以整合在一起变成$\sum_{i=1}^M(\frac{1}{1+exp(y^{(i)}w^Tx^{(i)})}-1)y^{(i)}x^{(i)}$，梯度计算里面最主要的就是矩阵乘法，一般的做法都是想办法将矩阵切割成大小合适的块。针对二分类，现在有M个样本，N个特征，假如有m*n个计算节点，并且将计算节点排列成m行n列，那么每个节点分配M/m个样本，N/n个特征，如下图所示。

图6 并行LR的数据分割(图片来源[20])

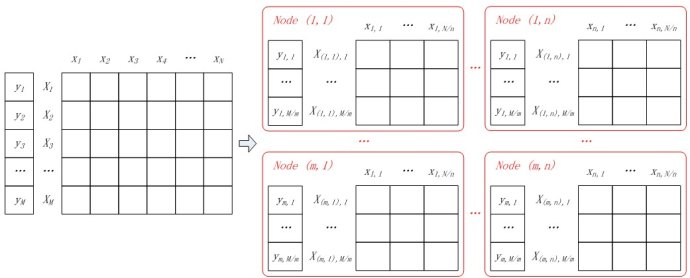
原文的标示我不太习惯，下面都改成了ij，并画出了矩阵运算的过程图。其中$X_{(i,j)}, i\in[1, m],j\in[1,n]$表示输入数据被分块后的第i行第j列的块。

$X_{(i,j),k}$表示这个块中的第k行，$W_j$表示参数的第j块。

第一步计算

$$d_{(i,j),k}=W^T_jX_{(i,j),k}$$

第二步计算

$$d_{i,k} = \sum_{j=1}{n}d_{(i,j),k}$$

图7 并行LR的求梯度12步

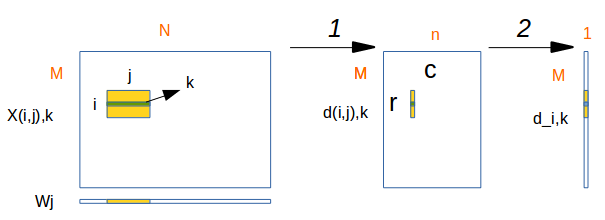
第三步计算

$$G_{(i,j)} = \sum_{k=1}^{M/m}(\frac {1}{1+exp(y_{i,k} d_{i,k})} - 1) y_{i,k}X_{(i,j),k}$$

第四步计算

$$G_{j} = \sum_{i=1}^mG_{(i,j)}$$

图6 并行LR的求梯度34步

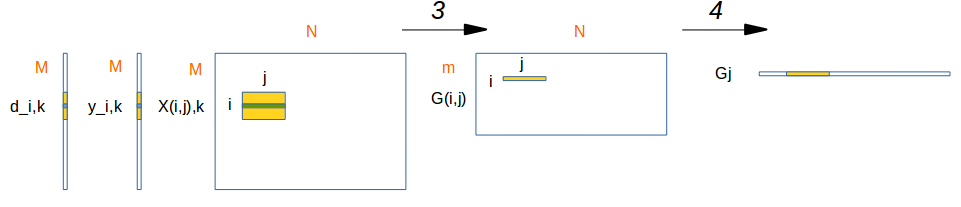
从而，经过上面的分解步骤可以将逻辑回归来做并行化计算。

7. 总结

这篇文章写了好几天，有时候写着写着就把自己绕进去了，因为可以展开说的地方太多了，写完这些内容，我又找了一些面试题看了看，理论部分基本上都能覆盖到了，但是涉及到真正的应用还是要再花时间去了解，最后的并行化理解还不够透彻，矩阵乘法我用gpu实现过，但是并没有接触过海量的数据，也不知道真正的问题会发生在什么地方。逻辑回归可以从很多方面来解释来理解，确实是个很美丽的算法。