最近两天研究了一下EM算法,主要是基于《统计学习方法》和论文《What is the expectation maximization algorithm?》[1],但是对两个文章里面给的实例求解过程都比较的困惑,搜索网上的一些博客也没有找到对应的求解过程,自己就仔细研究了一下,中间也遇到了一些坑,现在把解题思路给出来。因为书上和网上的博客[2]对EM算法的推导和证明解释的非常清楚,本文就不做解释了,如果对EM算法原理不清楚的建议先看看《统计学习方法》第9章或者博客[2][3]。本文只给出两个文章中的例子的求解过程。
(题目我会列出来,如果不是看这个两个文章而了解EM算法的也不要紧,题目是通用的)
本文中观测数据记为Y(因为两个例子都是输出是观测数据),隐藏变量(未观测变量)记为z,模型参数记为$\theta$。
1.三硬币模型
假设有三枚硬币A、B、C,每个硬币正面出现的概率是$\pi、p、q$。进行如下的掷硬币实验:先掷硬币A,正面向上选B,反面选C;然后掷选择的硬币,正面记1,反面记0。独立的进行10次实验,结果如下:1,1,0,1,0,0,1,0,1,1。假设只能观察最终的结果(0 or 1),而不能观测掷硬币的过程(不知道选的是B or C),问如何估计三硬币的正面出现的概率?
首先针对某个输出y值,它在参数$\theta (\theta=(\pi, p, q))$下的概率分布为
$$
P(y|\theta )=\sum_{z}P(y,z|\theta)=\sum_{z}P(z|\theta)P(y|z, \theta) = \pi p^y (1-p)^{1-y} + (1-\pi) q^y (1-q)^{1-y}
$$
从而针对观测数据$Y=(y_1, y_2, \cdot\cdot\cdot, y_n)^T$的似然函数为
$$
P(Y|\theta ) =\sum_{z}P(Y,z|\theta)=\sum_{z}P(z|\theta)P(Y|z, \theta) = \prod _{j=1} ^{n} \pi p^y_j (1-p)^{1-y_j} + (1-\pi) q^y_j (1-q)^{1-y_j}
$$
因此本题的目标是求解参数$\theta$的极大似然估计,即$\hat{\theta} = \underset{\theta }{argmax}logP(Y|\theta)$。直接对连乘的似然函数求导太复杂,所以一般用极大似然估计都会转化成对数似然函数,但是就算转化成了求和,如果这个式子对某个参数(例如$\pi$)求导,由于这个式子中有“和的对数”,求导非常复杂。因此这个问题需要用EM算法来求解。
E步:根据EM算法,在这一步需要计算的是未观测数据的条件概率分布,也就是每一个$P(z|y_j, \theta)$,$\mu^{i+1}$表示在已知的模型参数$\theta^i$下观测数据$y_j$来自掷硬币B的概率,相应的来自掷C的概率就是$1-\mu^{i+1}$。
$$\mu ^{i+1} = \frac {\pi^i ({p^i})^{y_j}(1-p^i)^{1-y_j}} {\pi^i ({p^i})^{y_j}(1-p^i)^{1-y_j} + (1-\pi^i) ({q^i})^{y_j} (1-q^i)^{1-y_j}}$$
这里的分子就是z取掷硬币B和y的联合概率分布,需要注意的是,这里的$\mu^{i+1}$通过E步的计算就已经是一个常数了,后面的求导不需要把这个式子代入。
M步:针对Q函数求导,Q函数的表达式是
$$Q(\theta, \theta^i) = \sum_{j=1}^N \sum_{z} P(z|y_j, \theta^i)logP(y_j, z|\theta)=\sum_{j=1}^N \mu_jlog(\pi p^{y_j}(1-p)^{1-y_j}) + (1-\mu_j)log((1-\pi) q^{y_j} (1-q)^{1-y_j})] $$
最开始求导犯了一个大错,没有将表达式展开来求,这样就直接默认$\mu_j$是一个系数,求导将它给约去了,这样就得不到最后的结果。
$$\frac{\partial Q}{\partial \pi} = (\frac{\mu_1}{\pi} - \frac{1-\mu_1}{1-\pi})+\cdot \cdot \cdot + (\frac{\mu_N}{\pi} - \frac{1-\mu_N}{1-\pi}) = \frac{\mu_1-\pi}{\pi(1-\pi)} + \cdot \cdot \cdot + \frac{\mu_N-\pi}{\pi(1-\pi)} = \frac{\sum _{j=1} ^N\mu_j-N\pi}{\pi(1-\pi)}$$
再令这个结果等于0,即获得$\pi^{i+1} = \frac{1}{N}\sum_{j=1}^{N}\mu_j^{i+1}$,其他两个也同理。
2.两硬币模型
假设有两枚硬币A、B,以相同的概率随机选择一个硬币,进行如下的掷硬币实验:共做5次实验,每次实验独立的掷十次,结果如图中a所示,例如某次实验产生了H、T、T、T、H、H、T、H、T、H,H代表证明朝上。a是在知道每次选择的是A还是B的情况下进行,b是在不知道选择的硬币情况下进行,问如何估计两个硬币正面出现的概率?
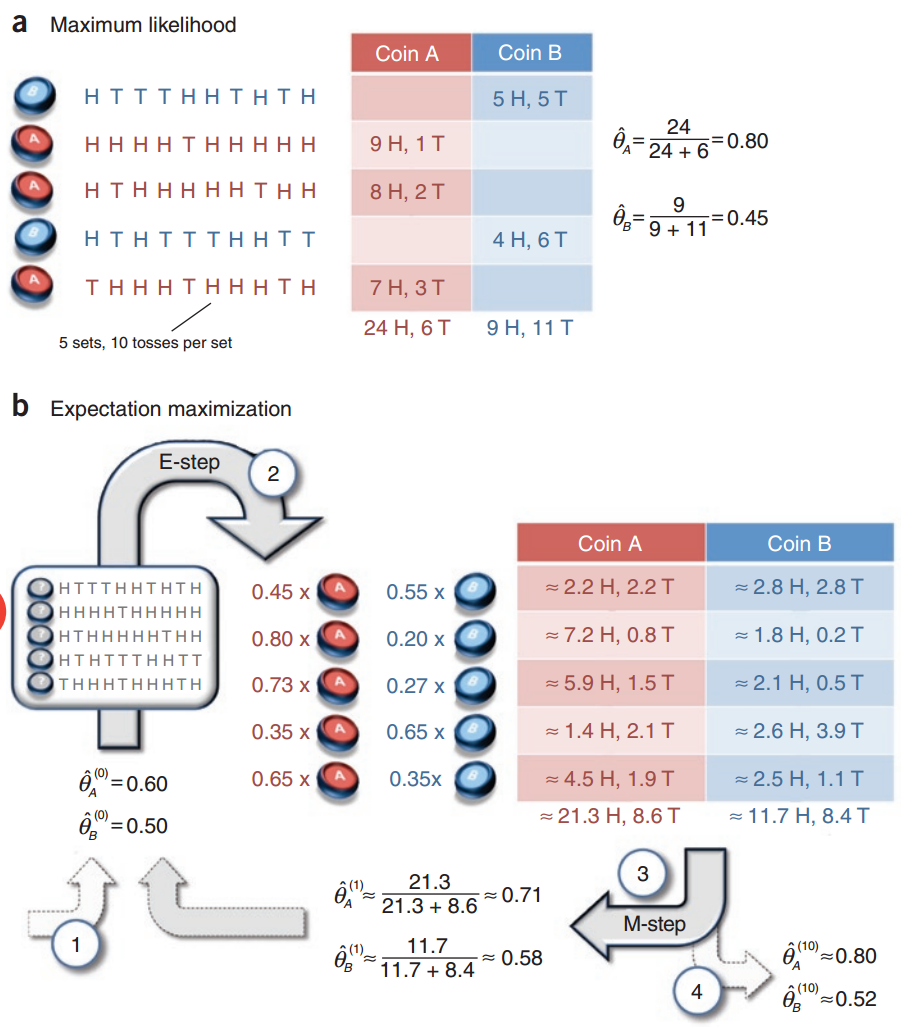
针对a情况,已知选择的A or B,重点是如何计算输出的概率分布,论文中直接统计了5次实验中A正面向上的次数再除以总次数作为A的$\hat{\theta_A}$,这其实也是极大似然求导求出来的。
$$\underset{\theta }{argmax}logP(Y|\theta) = log((\theta_B^5(1-\theta_B)^5) (\theta_A^9(1-\theta_A))(\theta_A^8(1-\theta_A)^2) (\theta_B^4(1-\theta_B)^6) (\theta_A^7(1-\theta_A)^3) ) = log( (\theta_A^{24}(1-\theta_A)^6) (\theta_B^9(1-\theta_B)^{11}) )$$
上面这个式子求导之后就能得出$\hat{\theta_A} = \frac{24}{24 + 6} = 0.80$以及$\hat{\theta_B} = \frac{9}{9 + 11} = 0.45$。
针对b情况,由于并不知道选择的是A还是B,因此采用EM算法。
E步:计算在给定的$\hat{\theta_A^{(0)}}$和$\hat{\theta_B^{(0)}}$下,选择的硬币可能是A or B的概率,例如第一个实验中选择A的概率为(由于选择A、B的过程是等概率的,这个系数被我省略掉了)
$$P(z=A|y_1, \theta) = \frac {P(z=A, y_1|\theta)}{P(z=A,y_1|\theta) + P(z=B,y_1|\theta)} = \frac{(0.6)^5*(0.4)^5}{(0.6)^5*(0.4)^5+(0.5)^{10}} = 0.45$$
M步:针对Q函数求导,在本题中Q函数形式如下,参数设置参照例1,只是这里的$y_j$代表的是每次正面朝上的个数。
$$Q(\theta, \theta^i) = \sum_{j=1}^N \sum_{z} P(z|y_j, \theta^i)logP(y_j, z|\theta)=\sum_{j=1}^N \mu_jlog(\theta_A^{y_j}(1-\theta_A)^{10-y_j}) + (1-\mu_j)log(\theta_B^{y_j}(1-\theta_B)^{10-y_j})]$$
从而针对这个式子来对参数求导,例如对$\theta_A$求导
$$\frac{\partial Q}{\partial \theta_A} = \mu_1(\frac{y_1}{\theta_A}-\frac{10-y_1}{1-\theta_A}) + \cdot \cdot \cdot + \mu_5(\frac{y_5}{\theta_A}-\frac{10-y_5}{1-\theta_A})
= \mu_1(\frac{y_1 - 10\theta_A} {\theta_A(1-\theta_A)}) + \cdot \cdot \cdot +\mu_5(\frac{y_5 - 10\theta_A} {\theta_A(1-\theta_A)}) = \frac{\sum_{j=1}^5 \mu_jy_j - \sum_{j=1}^510\mu_j\theta_A} {\theta_A(1-\theta_A)}$$
求导等于0之后就可得到图中的第一次迭代之后的参数值$\hat{\theta_A^{(1)}} = 0.71$和$\hat{\theta_B^{(1)}} = 0.58$。
这个例子可以非常直观的看出来,EM算法在求解M步是将每次实验硬币取A或B的情况都考虑进去了。
3.小结
EM算法将不完全数据补全成完全数据,而E步并不是只取最可能补全的未观测数据,而是将未观测的数据的所有补全可能都计算出对应的概率值,从而对这些所有可能的补全计算出它们的期望值,作为下一步的未观测数据。至于为什么取期望,一是因为这个未观测数据本身就是基于一组不完全正确的参数估计出来的,例如三硬币例子假如每次在进行maximization之前都只取某一个值(极端一点,每次结果都是认为B是最可能的观测数据,而不算C),那么在更新参数时,也只有B的参数在更新。二是这种情况下JENSEN不等式不成立,那么对$\theta$的似然函数变换形式就不成立,收敛也不成立。
这两个例子想明白之后求解实际上非常简单,所以很多博主并没把它们列出来,但如果一开始思考的方向不对就会浪费很多时间,当我把上面的过程想清楚之后再去求解别的例子,发现很轻松就能解出来。当然EM算法的核心还是证明和推导,这点别的文章讲的非常清晰了我就不赘述了。这也是数学上常用的思路,当无法直接对某个含参式子求极大值时,考虑对它的下界求极大值,当确定下界取极大值的参数时也能让含参式子值变大,也就是不断求解下界的极大值逼近求解对数似然函数极大化(李航.《统计学习方法》)。
如果本文有错误,请一定要指出来,感谢~
4.参考:
[1] What is the expectation maximization
algorithm?
[3] 从最大似然到EM算法浅解