基于Policy Gradient实现CartPole

【转载请注明出处】chenrudan.github.io

8月的时候把David silver的强化学习课上了，但是一直对其中概念如何映射到现实问题中不理解，半个月前突然发现OpenAI提供了一个python库Gym，它创造了强化学习的environment，可以很方便的启动一个强化学习任务来自己实现算法(新智元OpenAI简介[1])，并且提供了不少可以解决的问题来练手https://openai.com/requests-for-research/。本文针对如何解决入门问题CartPole，来解释一下怎么将之前课上的算法转化成实现代码。这里强烈推荐一下官网的教程http://kvfrans.com/simple-algoritms-for-solving-cartpole/，因为这个作者只是个高中生T^T…

建了一个强化学习讨论qq群，有兴趣的可以加一下群号595176373或者扫描下面的二维码。

1. Gym库

它提供了一些函数接口，模拟了强化学习问题中environment，当向它传递一个动作，它相应会返回执行这个动作后的状态、奖赏等。

#启动某种环境
env = gym.make('CartPole-v0') 
#针对传进来的动作返回状态observation等
observation, reward, done, info = env.step(action)

执行pip install gym即可安装，https://gym.openai.com/docs中有实例，复制代码运行即可检查是否安装成功。此外提供了env.monitor来记录下算法执行过程，它会保存为.mp4文件，然后上传到OpenAI网站上可以检查执行效率，上传可以通过执行代码中加入api_key(鉴别用户)，我是直接把api_key写入了~/.bashrc文件中即”export OPENAI_GYM_API_KEY=”。

2. CartPole问题

CartPole的玩法如下动图所示，目标就是保持一根杆一直竖直朝上，杆由于重力原因会一直倾斜，当杆倾斜到一定程度就会倒下，此时需要朝左或者右移动杆保证它不会倒下来。我们执行一个动作，动作取值为0或1，代表向左或向右移动，返回的observation是一个四维向量，reward值一直是1，当杆倒下时done的取值为False，其他为True，info是调试信息打印为空具体使用暂时不清楚。如果杆竖直向上的时间越长，得到reward的次数就越多。

#从动作空间中采样一个动作
action = env.action_space.sample()
observation, reward, done, info = env.step(action)
print observation

结果是[-0.061586 -0.75893141 0.05793238 1.15547541]。

图1 CartPole示意图

3. 三种解法

目的是在不同状态下执行出合适的action，代码中要做的就是替换掉采样这一行，用policy来决定执行什么动作。也就是说此处需要决定policy的形式，官网给出了两种思路，已知policy的输入是当前所处的状态observation，输出是action的取值即0 or 1，observation是一个四维向量，如果对这个向量求它的加权和，就可以得到一个值，那么就可以根据加权和的符号来决定action，同样可以用sigmoid函数当成二分类问题。基于这两种policy可以得到下面三种解法，核心就在于通过改变加权的权重值就能改变policy。

3.1 Random Guessing Algorithm & Hill Climbing Algorithm

由于policy中权重也是一个四维向量，如果随机给四维向量赋值，有机会得到比较好的policy。首先先实现一个函数用来衡量给定的某组权重效果如何，函数返回值是这组权重下得到的奖赏，意义是杆维持了多长时间未倒下，代码如下。

def evaluate_given_parameter_by_sign(env, weight):
    #启动初始状态
    observation = env.reset()
    #这组参数返回的总reward
    total_reward = 0.
    for t in range(1000):
        #这个渲染函数就是实时展示图1，如果隐藏，代码正常执行，但是不会显示图1了
        env.render()
        weighted_sum = np.dot(weight, observation)
        #根据符号policy选出action
        if weighted_sum >= 0:
            action = 1 
        else:
            action = 0 
    
        observation, reward, done, info = env.step(action)
        total_reward += reward
        if done:
            break
    return total_reward

然后要改变权重，这里试验了两种方法，一种是random guess，即随机给四维权重weight赋值，一种是hill climbing，即给当前最好的权重加上一组随机值，如果加上这组值持续时间变长了那么就更新最好的权重，如果没有变的更好就不更新。

def random_guess():
    env = gym.make('CartPole-v0')
    np.random.seed(10)
    best_reward = -100.0

    for iiter in xrange(1000):
        #####random guess随机初始化权重weight####
        weight = np.random.rand(4)
        #####

        ####hill climbing给best weight加随机值
        weight = best_weight + np.random.normal(0, 0.01, 4)
        #####

        cur_reward = evaluate_given_parameter_by_sign(env, weight)
        if cur_reward > best_reward:
            best_reward = cur_reward
            best_weight = weight

        if best_reward == 1000:
            break
        
    print("XXX algorithm best reward", best_reward)
    print("XXX algorithm best weight", best_weight)

3.2 Policy Gradient

上面的两种方法都是在随机的改变权重，针对这种参数非常少的情况确实能得到不错的效果，但是一旦参数数目增多，这种方式耗时非常大，一点也不实用。而第七课[2]讲解了两种Policy Gradient的方法，分别是Monte-Carlo Policy Gradient和Actor-Critic Policy Gradient。我们知道衡量policy好坏有三种方法，一是在某个状态下和该policy作用下能获得的值函数值，一是该policy作用下能获得的所有状态的期望值函数，一是在该policy作用下能获得的所有状态的期望immdiate reward，并且推导出了这三种方法的统一导数形式，即衡量policy的目标函数导数为$\bigtriangledown _{\theta}J(\theta) = E_{\pi_{\theta}}[\bigtriangledown _{\theta}log\pi_{\theta}(s,a)Q^{\pi_{\theta}(s,a)}]$，这个式子也就是policy gradient。

根据题目的意思，此处的policy换成逻辑回归，即$\pi_{\theta}(s,a) = \frac{1}{1 + e^{-wx}}$那么式子中$\bigtriangledown _{\theta}log\pi_{\theta}(s,a) = (1-pi)*(-x)$。在第一种方法中用直接用immdiate reward代替$Q{\pi_{\theta}(s,a)}$，所以在本例中就是直接取1。

首先定义一下选择action的函数，也就是利用sigmoid函数进行二分类。

def choose_action(weight, observation):
    weighted_sum = np.dot(weight, observation)
    pi = 1 / (1 + np.exp(-weighted_sum))
    if pi > 0.5:
        action = 1
    else:
        action = 0
    return pi, action

由于Monte-Carlo方法中需要先基于某组参数算出一个episode，再基于这个episode来更新policy的参数，所以需要实现一个函数产生一个episode。

def generate_episode(env, weight):
    episode = []
    pre_observation = env.reset()

    t = 0
    #generate 1 episodes for training.
    while 1:
        #env.render()
        pi, action = choose_action(weight, pre_observation)
    
        observation, reward, done, info = env.step(action)
        #将这个episode的每一步产生的数据保存下来
        episode.append([pre_observation, action, pi, reward])
        pre_observation = observation
    
        t += 1
        if done or t > 1000:
            break
    return episode

从而可以实现第七课中Monte-Carlo的更新方法。

def monte_carlo_policy_gradient(env):

    learning_rate = -0.0001
    best_reward = -100.0

    weight = np.random.rand(4)

    for iiter in xrange(1000):

        cur_episode = generate_episode(env, weight)
        for t in range(len(cur_episode)):
             
            observation, action, pi, reward = cur_episode[t]

            #根据第七课的更新公式
            weight += learning_rate*(1-pi)*np.transpose(-observation)*reward

    #衡量算出来的weight表现如何
    cur_reward = evaluate_given_parameter_sigmoid(env, weight)
    print 'Monte-Carlo policy gradient get reward', cur_reward

而针对Actor critic的方法，则是把值函数$Q{\pi_{\theta}(s,a)}$也当成observation的含参函数，且直接把observation的加权和当成值函数的取值，那么也就能由第七课的更新公式来同时更新值函数和policy的参数。代码如下:

def actor_critic_policy_gradient(env):
    gamma = 1

    p_weight = np.random.rand(4)
        
    #值函数的权重
    v_weight = np.random.rand(4)

    p_learning_rate = -0.0001
    v_learning_rate = -0.0001

    done = True

    for iiter in xrange(1000):

        t = 0
        while 1:
            if done:
                print 'start new training...'
                print 'p_weight', p_weight
                print 'v_weight', v_weight

                pre_observation = env.reset()
                pre_pi, pre_action = choose_action(p_weight, pre_observation)
        
                pre_phi = pre_observation
                pre_q = np.dot(v_weight, pre_phi)

            #env.render()

            observation, reward, done, info = env.step(pre_action)

            pi, action = choose_action(p_weight, observation)
            
            phi = observation
            q = np.dot(v_weight, phi)

            delta = reward + gamma*q - pre_q

            p_weight += p_learning_rate*(1-pre_pi)*np.transpose(-pre_observation)*pre_q

            v_weight += v_learning_rate*delta*np.transpose(pre_phi)

            pre_pi = pi
            pre_observation = observation
            pre_q = q
            pre_phi = phi
            pre_action = action

            t += 1
            if done:
                break

    cur_reward = evaluate_given_parameter_sigmoid(env, p_weight)
    print 'Actor critic policy gradient get reward', cur_reward

4.提交到OpenAI

上面的代码实现以后，就能够提交到OpenAI的网站上去评估效果如何，首先加上两行代码，变成下面的样子。

env = gym.make('CartPole-v0')
env.monitor.start('cartpole-hill/', force=True)
actor_critic_policy_gradient(env)
env.monitor.close()

这会将训练过程记录下来生成.mp4文件，如果像我这样将api_key写入~/.bashrc，就可以直接执行下面代码提交给OpenAI。

1	gym.upload('cartpole-hill')

最后在网站上就能看到如下的结果。

图2 结果提交成功图

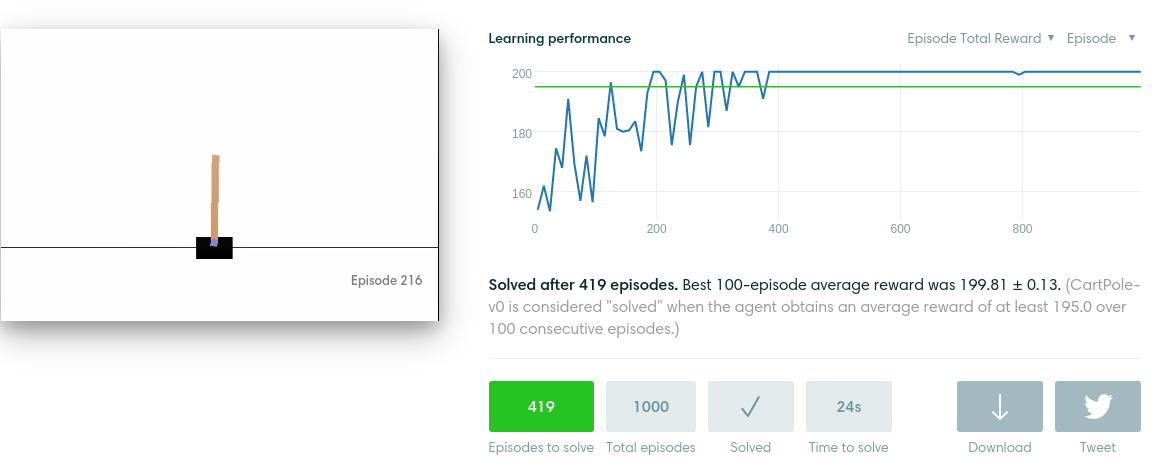
5.小结

我的policy gradient是完全按照第七课的内容实现的，但是实际上效果还不够好，并且非常依赖初始值，初始值好就很快收敛，不好就会一直恶性循环。总之感觉这个网站还是很有意思的，值得去玩一玩，文中的代码在这里。

[1] 【重磅】马斯克的AI野心——OpenAI Gym系统深度解析

[2] 【David Silver强化学习公开课之七】Policy Gradient