【转载请注明出处】chenrudan.github.io
本文是David Silver强化学习公开课第八课的总结笔记。这一课主要讲了如何拟合environment模型,通过有监督的方式来更新model,以及如何基于学习的model来找policy/value function,主要谈到了Monte-Carlo Tree Search方法,并且将拟合model和求解value function结合起来实现Dyna算法。
本课视频地址:RL Course by David Silver - Lecture 8: Integrating Learning and Planning
本课ppt地址:http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching_files/dyna.pdf
文章的内容是课程的一个总结和讨论,会按照自己的理解来组织。个人知识不足再加上英语听力不是那么好可能会有一些理解不准的地方,欢迎一起讨论。
建了一个强化学习讨论qq群,有兴趣的可以加一下群号595176373或者扫描下面的二维码。

1.内容回顾
前面两节课是将policy和value function表达成参数形式,从而通过更新参数来解决MDP问题,而本课则是希望拟合出未知environment的model,即知道environment是如何转移状态和反馈reward,那么就能从model中找到合适的policy和value function,这一步称为planning。本课的标题中learn指的是在不学习model的情况下对policy和value function建模的行为,而plan就是学习model,并从model中推断出policy和value function,后者也叫model-based reinforcement learning。
environment的参数化好处在于,避免了状态多policy复杂难学,它像在模拟出游戏的规则,这样就能通过搜索树的方式获得value function,并且能够通过监督学习方式来学习model。例如输入是状态$s$输出是状态$s’$,此处就能给一定的监督信息,说明$s’$取什么样的值比较好。而缺点在于用一个近似的model来构造一个近似的value function,两个近似都会存在一定的误差。
2.Model-Based Reinforcement Learning
model的形式可以表现为$S,A,P,R$,假设状态集和动作集是已知的,把状态转移和奖赏表示成状态和动作的独立概率分布为$P[S_{t+1}, R_{t+1}|S_t, A_t] = P[S_{t+1}|S_t, A_t]P[R_{t+1}|S_t,A_t]$。目标就是从一段执行序列中$S_1,A_1,R_2,…,S_T$来估计model,这样就能看成一个监督问题,把$S_t,A_t$当成模型输入,那么即$R_{t+1},S_{t+1}$就能看成模型的输出。学习$R_{t+1}$是一个回归问题,可以用最小均方差等方法来解决,而学习$S_{t+1}$则是一个密度估计问题,可以用KL divergence等方法来解决。
举个例子,有两个状态$A,B$,有8条序列,分别是$(A,0,B,0),(B,1),(B,1),(B,1),(B,1),(B,1),(B,1),(B,0)$。数字代表这个状态下的reward,用最简单的建模方式,将所有转移过状态记录下来,reward平均一下。从样本中状态A肯定会转移到状态B,且reward均值是0,而状态B有6次reward是1,2次reward是0,平均一下得到有75%概率得到reward为1,就能得到右边的model图。
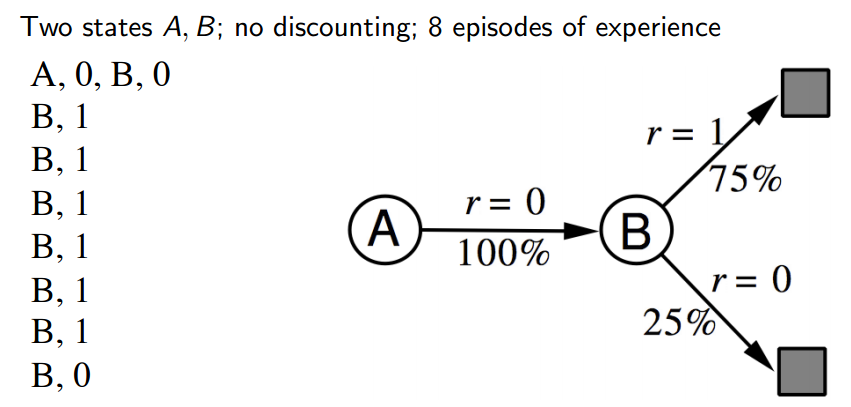
拟合好模型之后就是如何plan出相应的value function,最简单的planning方法就是从model中采样出一些样本,然后基于这些样本当成model-free的强化学习问题来解决,即之前课上的Monte-Carlo control、Sarsa等算法,这种方法叫Sample-based planning。针对之前的例子,假如采样得到8个样本$(B,1),(B,0),(B,1),(A,0,B,1),(B,1),(A,1,B,1),(B,1),(B,0)$,用Monte-Carlo learning来分析,A状态出现了两次,每次最终获得的reward是1,$V(A)=1$,而B状态则出现8次,6次reward为1,因此$V(B)=0.75$。
3.Integrated Architectures
从上面内容可以看出存在两种样本,一种是真实数据称为Real experience,一种是从model中采样出来的称为Simulated experience。
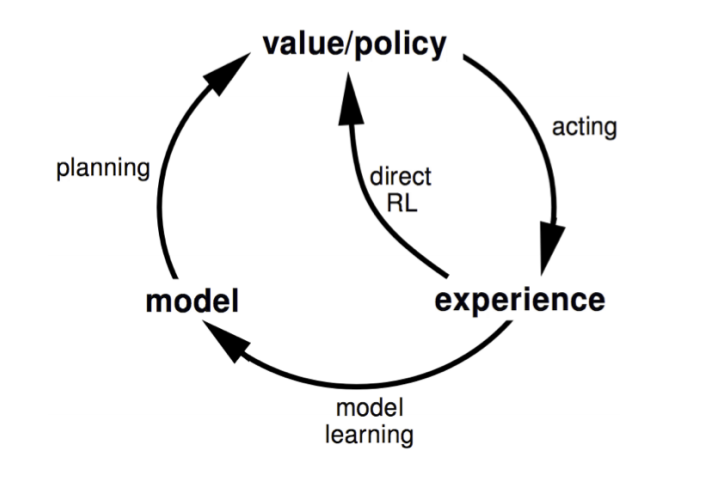
如果将learn和plan结合起来,即又学习model的形式,又学习value function或者policy,这也是一种方法,称为Dyna。如下图所示,experience包括real和simulated两种,既可以用real数据来直接学value function/policy,也可以将real数据用来学习model,然后由model产生simulated数据继续学value function/policy。结合Q-learning的算法流程如下。
- 针对集合$S$和$A$所有值初始化$Q(s,a)$和$Model(s,a)$
- 循环
- ==选择当前状态为$S$,通过$\epsilon-$greedy选择一个$A$
- ==执行$A$,获得reward R和下一个state $S’$(前两步都来自real experience)
- ==由Q-Learning更新动作值函数$Q(S,A) = Q(S,A) + \alpha[R+\gamma max_aQ(S’,A)-Q(S,A)]$
- ==由获得的$R,S’$来学习模型$Model(S,A)$
- ==循环n次
- ====随机选择一个$S$和$A$
- ====基于模型得到$R,S’$
- ====同样的方法更新动作值函数
3.Simulation-Based Search
上面的方法在plan值函数的时候,是随机选状态和动作再更新。但是在状态集常常会有比较关键的状态和没用的状态,那么就应该更多的关注重要的状态,将一个重要的状态作为根节点,由$Model(s,a)$得到从这个状态出发的搜索树,如下图。再从分支中选择一些episode来做model-free learning,如果选择的方法是Monte-Carlo control方法,那么整个算法就叫Monte-Carlo Search。
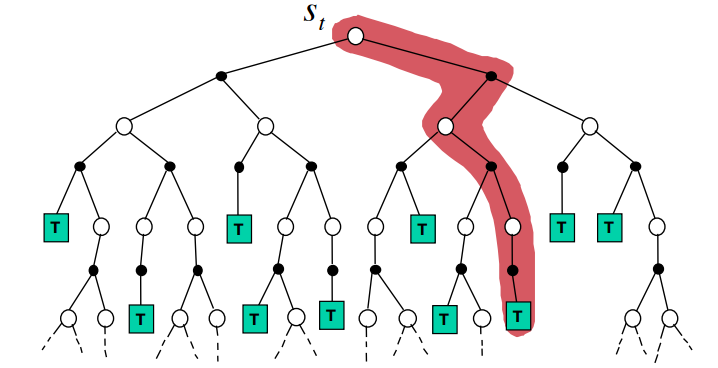
Monte-Carlo Tree Search算法的流程如下
- 给定一个model $M_v$
- 从一个重要状态出发$s_t$在当前的simulation policy下模拟出K个episodes,即得到$( s_t, A_t^k, R_{t+1}^k, S_{t+1}^k…,S_T^k) _{k=1}^K~M_v,\pi$
- 根据episodes构造搜索树
- 由Monte-Carlo Learning每次访问到$s,a$都记录一次最后求所有episodes的平均得到$Q(s,a) = \frac{1}{N(s,a)} \sum_{k=1}^K\sum_{u=t}^T 1(S_u,A_u=s,a)G_u$
- 然后由最大值函数得到当前最佳的action,即$a_t = \underset{a\in A}{argmax}Q(s_t,a)$
实际上就是将Monte-Carlo control应用到simulated experience上。
例如围棋中衡量一个位置$s$的好坏问题。这里的奖赏函数是中间时刻$R_t=0$,到达终止状态时如果是黑赢了$R_T=1$,如果是白赢了$R_T=0$。policy由两部分组成$\pi = (\pi_B,\pi_W)$分别是两个玩家落子策略,值函数(位置s的好坏)是当前状态下黑子赢的概率$v_{\pi}(s) = P[Black:wins|S=s]$,最大值函数是$v_*(s) = \underset{\pi_B}{max} :\underset{\pi_W}{min}v_{\pi}(s)$
如果将MC的部分改成用TD来更新$Q(s,a)$就是TD search。可以看出Dyna算法就是分了两次更新值函数。
[1] http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching_files/dyna.pdf